Dijkstra算法
Dijkstra算法是一种用于寻找带权重图中单源最短路径的经典算法。它适用于非负权重的图。算法的基本思想是从起点开始,逐步扩展到其他顶点,每次都选择当前距离最小的顶点进行扩展,直到所有顶点都被处理完毕。
在C++中,可以使用优先队列(通常使用std::priority_queue)来高效地实现Dijkstra算法。
代码实现
Graph类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| #include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <utility>
using namespace std;
const int INF = numeric_limits<int>::max();
class Graph {
int V;
vector<vector<pair<int, int>>> adj;
public:
Graph(int V);
void addEdge(int u, int v, int weight);
vector<int> dijkstra(int src);
};
Graph::Graph(int V) {
this->V = V;
adj.resize(V);
}
void Graph::addEdge(int u, int v, int weight) {
adj[u].emplace_back(v, weight);
}
|
Graph::dijkstra()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| vector<int> Graph::dijkstra(int src) {
vector<int> dist(V, INF);
dist[src] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
pq.push({0, src});
while (!pq.empty()) {
int u = pq.top().second;
int distance = pq.top().first;
pq.pop();
if (distance > dist[u]) continue;
for (auto& edge : adj[u]) {
int v = edge.first;
int weight = edge.second;
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push({dist[v], v});
}
}
}
return dist;
}
|
main函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| int main() {
int V = 9;
Graph g(V);
g.addEdge(0, 1, 4);
g.addEdge(0, 7, 8);
g.addEdge(1, 2, 8);
g.addEdge(1, 7, 11);
g.addEdge(2, 3, 7);
g.addEdge(2, 8, 2);
g.addEdge(2, 5, 4);
g.addEdge(3, 4, 9);
g.addEdge(3, 5, 14);
g.addEdge(4, 5, 10);
g.addEdge(5, 6, 2);
g.addEdge(6, 7, 1);
g.addEdge(6, 8, 6);
g.addEdge(7, 8, 7);
int src = 0;
vector<int> dist = g.dijkstra(src);
cout << "Vertex Distance from Source " << src << endl;
for (int i = 0; i < V; ++i) {
cout << i << " \t\t " << dist[i] << endl;
}
return 0;
}
|
解释
- Graph 类:
Graph(int V) 构造函数初始化图的顶点数,并设置邻接表的大小。addEdge(int u, int v, int weight) 方法添加一条从顶点 u 到顶点 v 的有向边,权重为 weight。dijkstra(int src) 方法实现Dijkstra算法,返回从源顶点 src 到其他所有顶点的最短路径距离。
- dijkstra 方法:
- 初始化距离数组
dist,所有顶点的初始距离设为无穷大,源顶点的距离设为0。
- 使用优先队列
pq 存储当前已知的最短距离和对应的顶点。
- 当队列不为空时,取出距离最小的顶点
u 和其距离 distance。
- 如果当前距离大于已知的最短距离,跳过该顶点。
- 对于顶点
u 的所有相邻顶点 v,如果通过顶点 u 可以到达顶点 v 并且距离更短,则更新 dist[v] 并将新的距离和顶点 v 加入优先队列。
- main 函数:
- 创建一个图实例,添加一些边。
- 调用
dijkstra 方法从源顶点 0 开始进行最短路径计算,并输出结果。
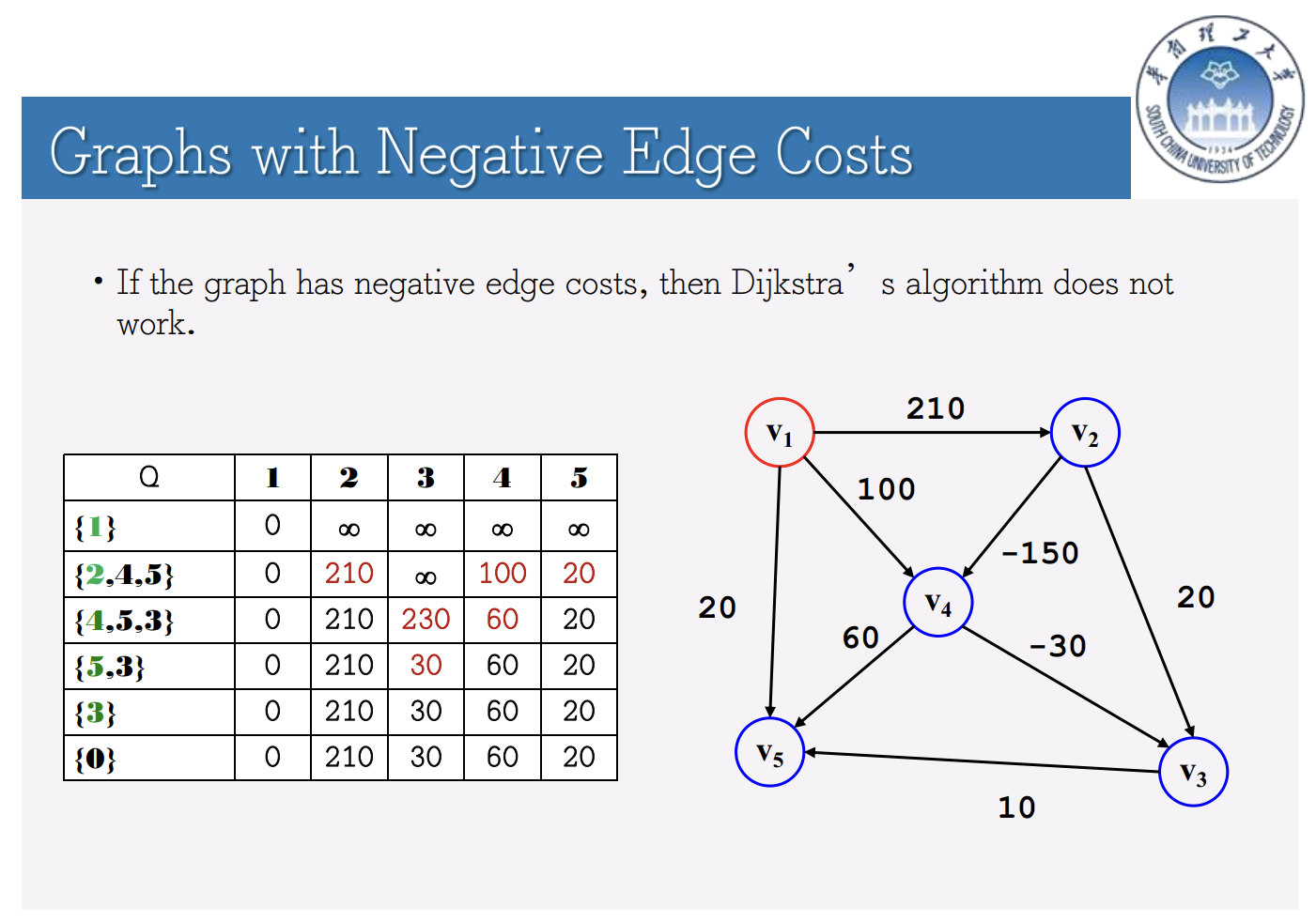
带负权的赋权图求最短路径
需要使用队列queue而不是优先队列priority_queue来实现
伪代码

例子