离散数学中的其中几种证明题
发表于|更新于|数学
|总字数:5|阅读时长:1分钟
(1)


结论:
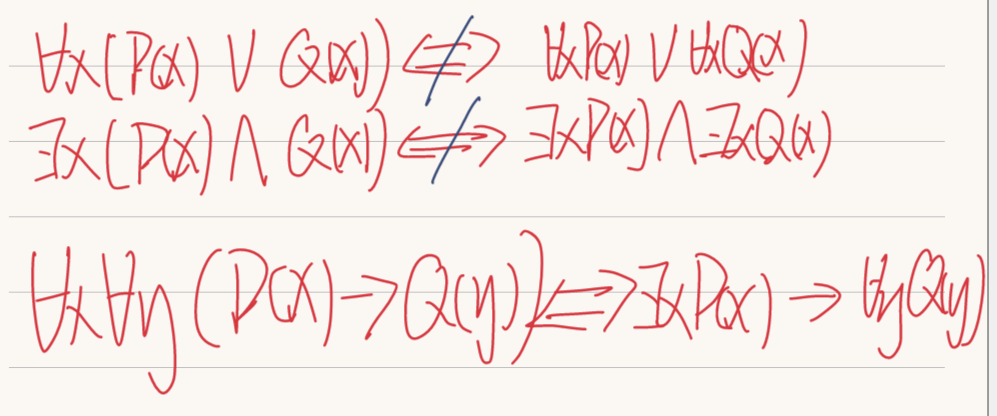
(2)

(3)

文章作者: Lee
版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Lee的学习之旅!
相关推荐

2024-12-16
一道关于足球的考察平面图知识的题目
题目及解答 关于平面图概念离散数学中的平面图是一种特殊的无向图,它可以在平面上绘制而没有任何边交叉。换句话说,一个图如果可以嵌入到平面中,即可以在不使边交叉的情况下画在平面上,则该图称为平面图。 平面图的一些重要概念和定理包括: 库拉托夫斯基定理:这是判断一个图是否为平面图的一个标准。根据这个定理,一个有限图是平面图当且仅当它不包含K₅(完全五边形)或K₃,₃(完全二分图,两边各有三个顶点)作为子图的细分。也就是说,不能通过增加顶点将这些图变成原图的子图。 欧拉公式:对于任何连通的平面图,设V为顶点数,E为边数,F为面数(包括外部无限面),则有 V - E + F =...
2024-12-13
证明无向图是连通图或者它的补图是连通图
补图的定义补图的数学定义为:对于一个给定的图G=(V,E),其补图G'=(V,E')是一个具有相同顶点集V的图,其中**E'是V中未出现在E中的所有可能边的集合**。换句话说,G'中的边是G中不存在的边。 例题: 证明过程要证明对于任何无向图G,要么G是连通的,要么它的补图G’是连通的,我们可以使用反证法。 定义: 一个无向图G=(V,E)是连通的,如果对于任意两个顶点u, v ∈ V,存在一条从u到v的路径。 无向图G的补图G’=(V,E’),其中E’包含所有不属于E的边,即如果(u,v) ∉ E,则(u,v) ∈ E’。 证明: 假设给定一个无向图G,它既不是连通图,其补图G’也不是连通图。这意味着在G中存在至少两个连通分量C1和C2,在G’中也存在至少两个连通分量C1’和C2’。 考虑G中的两个连通分量C1和C2,因为它们是不同的连通分量,所以不存在直接连接C1和C2中顶点的边,即对于所有的u ∈ C1和v ∈ C2,(u,v) ∉ E。根据补图的定义,这些不在E中的边都应该出现在E’中,即对于所有的u ∈ C1和v ∈...

2024-12-13
排序算法的复杂度
各类排序算法的复杂度 任何需要交换相邻元素进行排序的排序算法平均都需要Ω(N^2)时间证明:


