补图的定义

补图的数学定义为：对于一个给定的图G=(V,E)，其补图G'=(V,E')是一个具有相同顶点集V的图，其中**E'是V中未出现在E中的所有可能边的集合**。换句话说，G'中的边是G中不存在的边。

例题：

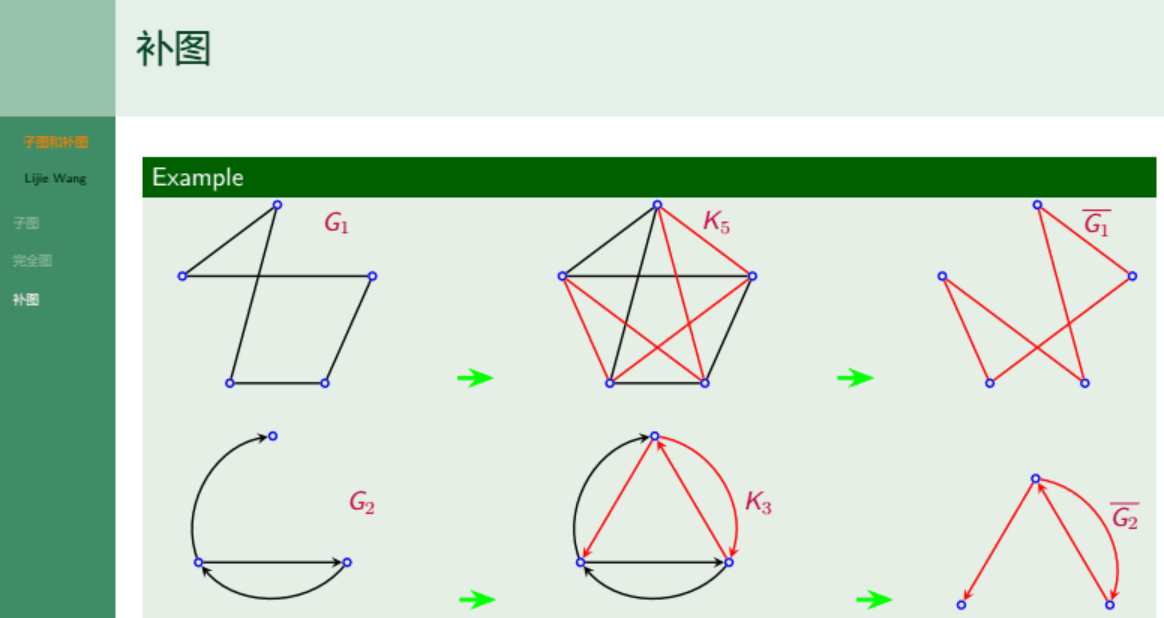
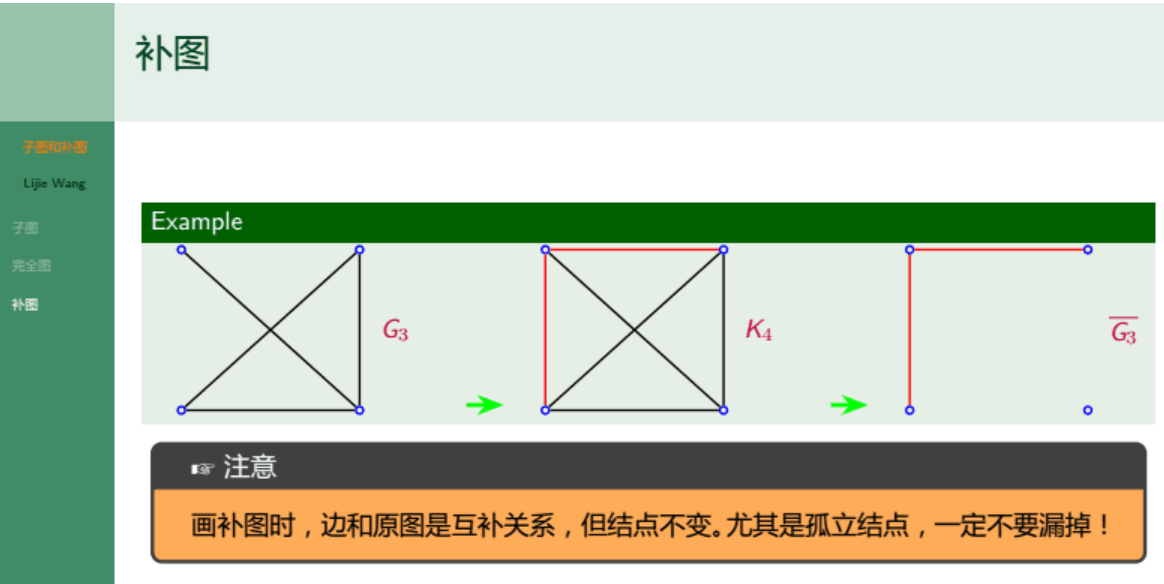
证明过程

要证明对于任何无向图G，要么G是连通的，要么它的补图G’是连通的，我们可以使用反证法。

定义：

  • 一个无向图G=(V,E)是连通的，如果对于任意两个顶点u, v ∈ V，存在一条从u到v的路径。
  • 无向图G的补图G’=(V,E’)，其中E’包含所有不属于E的边，即如果(u,v) ∉ E，则(u,v) ∈ E’。

证明：

假设给定一个无向图G，它既不是连通图，其补图G’也不是连通图。这意味着在G中存在至少两个连通分量C1和C2，在G’中也存在至少两个连通分量C1’和C2’。

考虑G中的两个连通分量C1和C2，因为它们是不同的连通分量，所以不存在直接连接C1和C2中顶点的边，即对于所有的u ∈ C1和v ∈ C2，(u,v) ∉ E。根据补图的定义，这些不在E中的边都应该出现在E’中，即对于所有的u ∈ C1和v ∈ C2，(u,v) ∈ E’。这意呀着C1和C2中的所有顶点在G’中都是互相连接的，因此在G’中应该存在一个连通分量包含了C1和C2的所有顶点。这与我们的假设矛盾，即G’不是连通图。

由此我们得出结论：如果G不是连通的，则G’必须是连通的。反之亦然，如果G’不是连通的，则G必须是连通的。因此，对于任何无向图G，要么G是连通的，要么它的补图G’是连通的。

请注意，这个证明假定了图G没有孤立的顶点（即度为0的顶点）。如果有孤立的顶点，那么该顶点将不会在G或G’中形成任何边，从而可能导致两者都不是严格意义上的连通图。然而，通常在讨论连通性时，孤立顶点被视作单独的连通分量处理。