原理

层次分析法（Analytic Hierarchy Process，简称AHP）是一种结构化的多准则决策制定方法。它是由美国运筹学家托马斯·萨蒂（Thomas L. Saaty）在20世纪70年代提出的。该方法通过将复杂的问题分解成多个层次的子问题，并对这些子问题进行两两比较，从而帮助决策者在多个备选方案中选择最优方案。

以下是使用层次分析法的基本步骤：

  1. 构建层次结构模型：
    • 目标层：明确决策的目标。
    • 准则层：确定达成目标所需的评价标准或准则。
    • 方案层：列出所有可行的备选方案。
  2. 构造判断矩阵： 对于每一层中的元素，根据其相对于上一层某一元素的重要性，进行两两比较，构造出一个正互反矩阵（即判断矩阵）。比较时通常采用Saaty的1-9标度法来量化相对重要性。
  3. 计算权重向量和一致性检验：
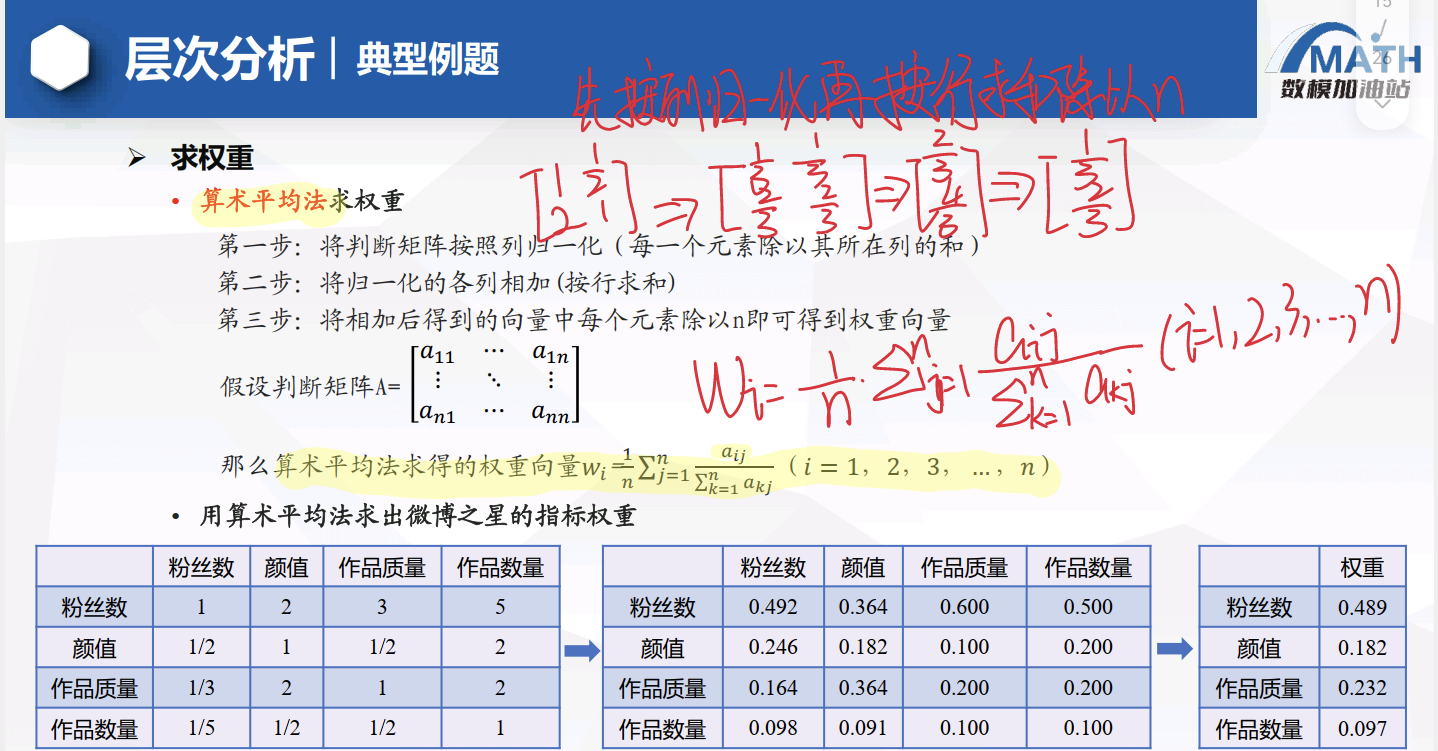
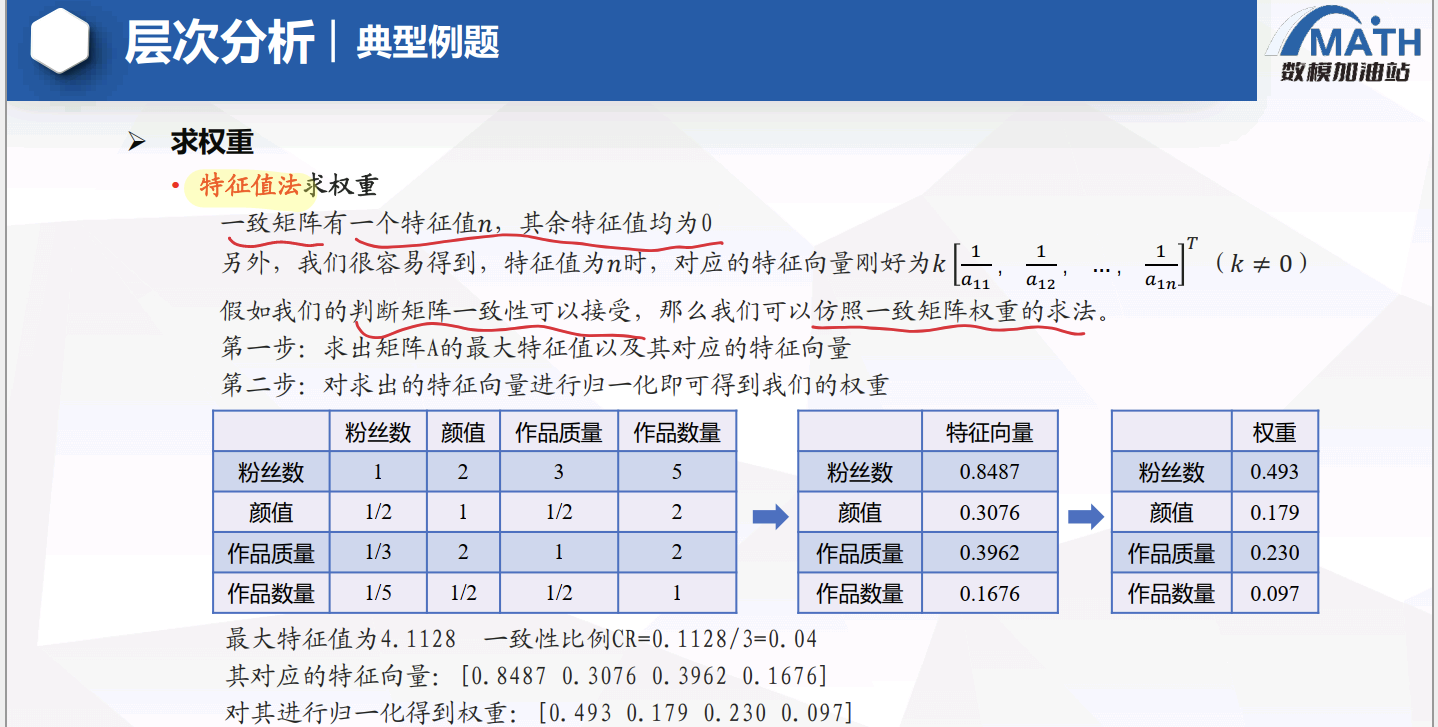
    • 计算每个判断矩阵的最大特征根及其对应的归一化特征向量，这个特征向量即为相应层各元素的权重向量。
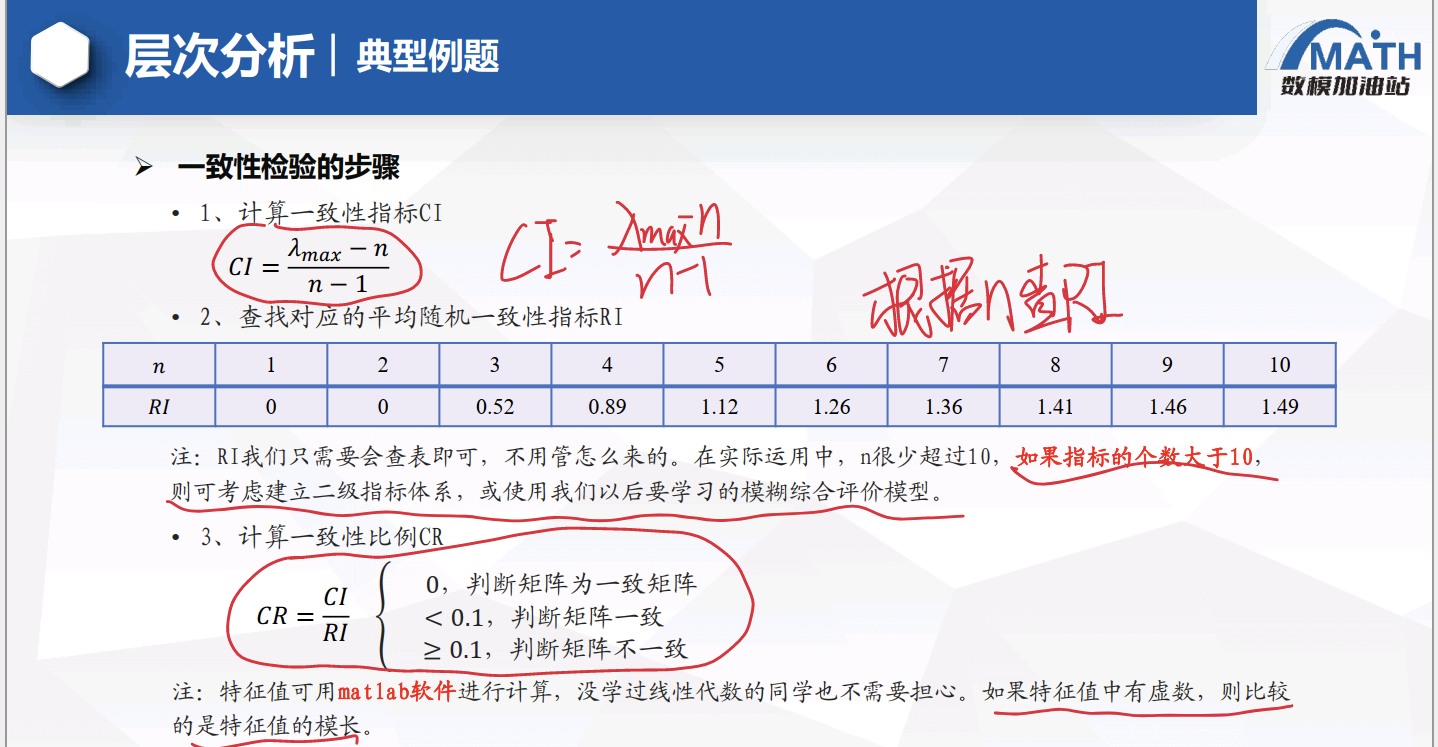
    • 进行一致性比率（Consistency Ratio, CR）检验，以确保判断矩阵的一致性达到可接受水平。如果CR小于0.1，则认为判断矩阵具有满意的一致性；否则需要调整判断矩阵，直到满足一致性要求。
  4. 层次总排序及组合权重计算：
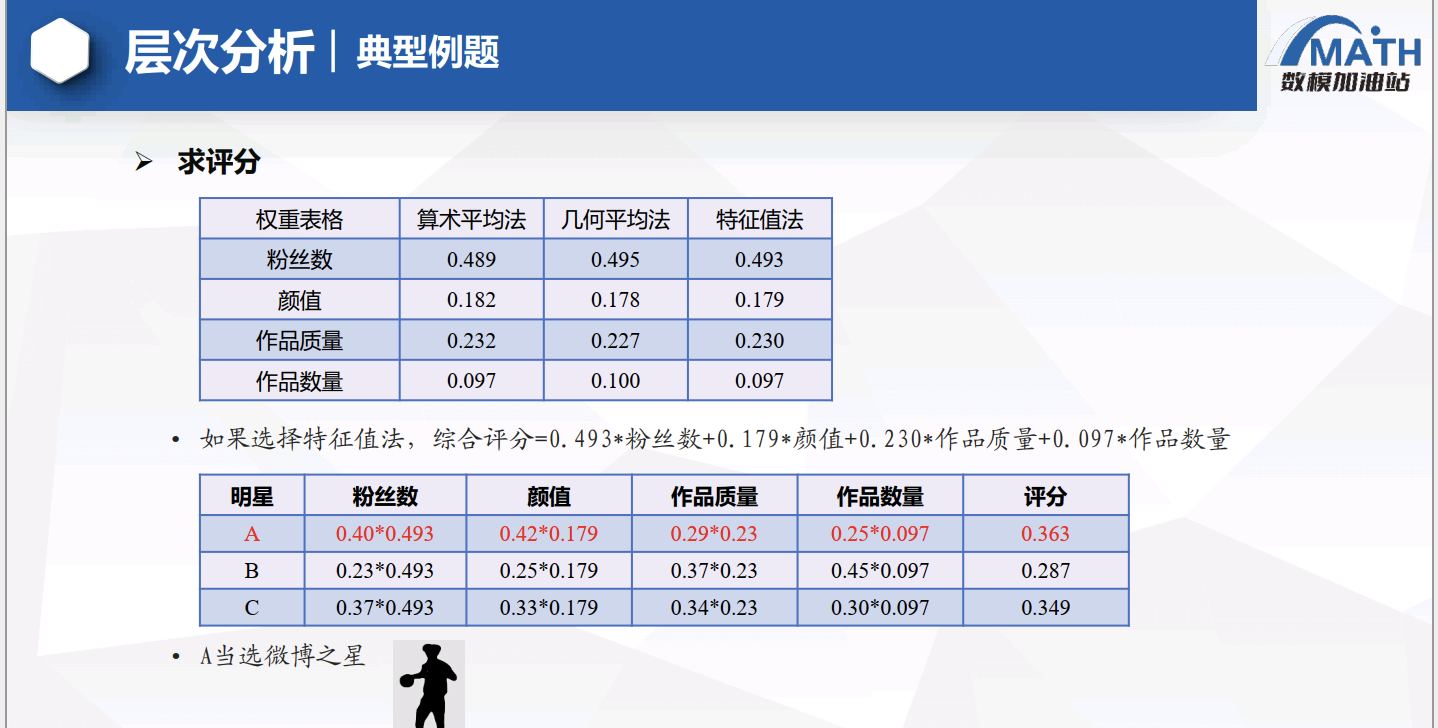
    • 从最高层到最低层逐层计算各元素的组合权重，即综合考虑所有准则后每个方案的总体优先级。
    • 最终得到各方案关于目标层的总排序，从而确定最优方案。
  5. 敏感性分析（可选）：
    • 分析当某些参数发生变化时，结果是否稳定，以评估决策过程的稳健性。

层次分析法的优势在于它能够处理定性和定量相结合的决策问题，提供了一种系统、直观的方法来表达复杂的决策过程。然而，它也存在一些局限性，例如主观因素影响较大、对于大规模问题可能变得难以管理等。因此，在应用AHP时，应结合实际情况和其他工具一起使用，以提高决策质量。

三种求权重的方法：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
%代码一致性检验
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 1/2;1/5 1/2 2 1]; 不符合一致性
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1]; 符合一致性
A = input('判断矩阵A=');    %输入判断矩阵
[n,n] = size(A);             %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A);              %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D));       %先求出每一列的最大值，再求最大值中的最大值
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  
%注意哦，这里的RI最多支持 n = 15
%这里n=2时，一定是一致矩阵，所以CI = 0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
    disp('因为CR<0.10，所以该判断矩阵A的一致性可以接受!');
else
    disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
end
%1.算术平均法计算权重
%输入样例：
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
A = input('判断矩阵A=');  %输入判断矩阵
ASum = sum(A,1);        %将判断矩阵每列求和
[n,n] = size(A);        %获取A的行和列，用于对ASum复制，对应位相除归一化
Ar = repmat(ASum,n,1);  %复制Asum Ar矩阵为n*n矩阵
Stand_A = A./Ar;        %归一化
ASumr = sum(Stand_A,2); %各列相加到同一行
disp(ASumr/n);          %将相加后得到的向量每个元素除以n可以得到权重向量
%2.几何平均法计算权重
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
clc;
A = input('判断矩阵A=');   %输入判断矩阵
[n,n] = size(A);            %获取A的行和列
prod_A = prod(A,2);         %将A中每一行元素相乘得到一列向量
prod_n_A = prod_A.^(1/n);   %将新的向量的每个分量开n次方等价求1/n次方
re_prod_A = prod_n_A./sum(prod_n_A);%归一化处理
disp(re_prod_A);            %展示权重结果
%3.特征值法计算权重
% A=[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1];
clc;
A = input('判断矩阵A=');    %输入判断矩阵
[n,n] = size(A);             %获取A的行和列
%求出最大特征值以及对应的特征向量
[V,D] = eig(A);              %V是特征向量 D是特征值构成的对角矩阵
Max_eig = max(max(D));       %先求出每一列的最大值，再求最大值中的最大值
[r,c] = find(Max_eig == D,1);%使用find()函数找出最大特征值对应的特征向量
%对特征向量进行归一化得到所需权重
disp(V(:,c)./sum(V(:,c)));

测试输入：

1
[1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1]

测试输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
一致性指标CI=
    0.0376
    
一致性比例CR=
    0.0423
    
因为CR<0.10，所以该判断矩阵A的一致性可以接受!

    0.4889
    0.1819
    0.2319
    0.0973
    
    0.4949
    0.1778
    0.2272
    0.1000
    
    0.4934
    0.1788
    0.2303
    0.0974