熵权法

原理

1. 熵权法介绍
   • 熵权法是一种客观赋权的方法，它依靠数据本身计算出权重，用于多指标综合评价。
   • 信息是系统有序程度的度量，而熵则是无序程度的度量。根据信息熵定义，可以使用熵值判断某个指标的离散程度。一个指标的离散程度越大，该指标对综合评价的影响也越大。
2. 模型引出
   • 提出了问题：如何确定不同指标在综合评价中的重要性（权重），以及主观方法的局限性。
   • 使用了一个帮助明星K选对象的例子来解释，当候选人在某一特征上差异很小，则该特征对于选择的重要性较低；反之，如果差异较大，则该特征更需要被重视。
3. 基本原理
   • 指标的变异程度越小，所反映的信息量也越少，对应的权值应越低。
   • 如果某项指标的值全部相等，那么该指标在综合评价中不起作用。
   • 可以用信息熵作为工具，通过计算各指标的熵值，进而计算出各个指标的权重。
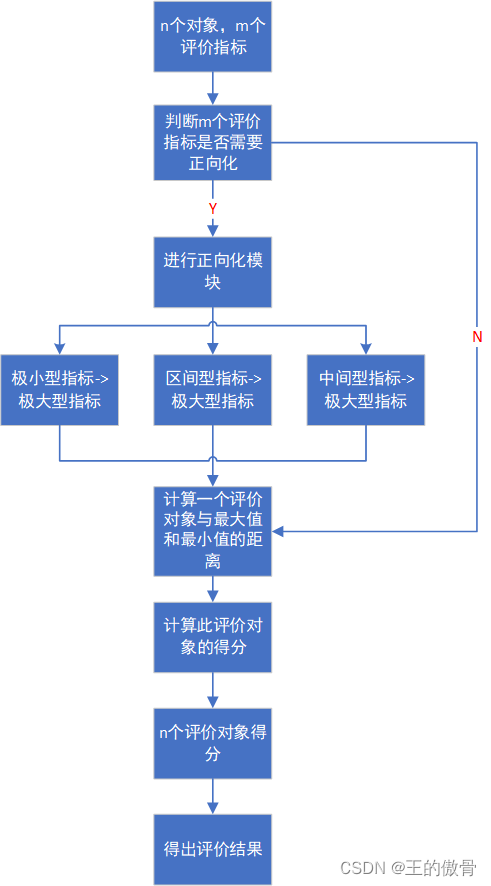
4. 基本步骤
   • 数据标准化：将原始数据进行标准化处理，以便于比较不同量纲的数据。
   • 计算比重：基于标准化后的数据，计算每个样本在每个指标下的相对比重。
   • 计算概率矩阵：根据比重计算每个样本在所有指标下的概率分布。
   • 计算熵权：利用信息熵公式计算每个指标的信息熵，并据此计算信息效用值和熵权。

代码

mylog

因为p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数

% 重新定义一个mylog函数，当输入的p中元素为0时，返回0
function [lnp] =  mylog(p)
n = length(p);   % 向量的长度
lnp = zeros(n,1);   % 初始化最后的结果
    for i = 1:n   % 开始循环
        if p(i) == 0   % 如果第i个元素为0
            lnp(i) = 0;  % 那么返回的第i个结果也为0
        else
            lnp(i) = log(p(i));  
        end
    end
end

Entropy_Method

%% 1.对正向化后的矩阵进行标准化
% X=[9 0 0 0 ;8 3 0.9 0.5;6 7 0.2 1]
clear,clc;
X=input('指标矩阵X='); 
[n,m] = size(X);
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)


%% 2.计算熵权
  
    D = zeros(1,m);  % 初始化保存信息效用值的行向量
    for i = 1:m
        x = Z(:,i);  % 取出第i列的指标
        p = x / sum(x);
        % 注意，p有可能为0，此时计算ln(p)*p时，Matlab会返回NaN，所以这里我们自己定义一个函数
        e = -sum(p .* mylog(p)) / log(n); % 计算信息熵
        D(i) = 1- e; % 计算信息效用值
    end
    W = D ./ sum(D);  % 将信息效用值归一化，得到权重    
disp('权重 W = ')
disp(W)

运行测试

指标矩阵X=[9 0 0 0 ;8 3 0.9 0.5;6 7 0.2 1]
标准化矩阵 Z = 
    0.6690         0         0         0
    0.5946    0.3939    0.9762    0.4472
    0.4460    0.9191    0.2169    0.8944

权重 W = 
    0.0086    0.3072    0.3933    0.2910