灰色关联分析

原理

灰色关联分析（Grey Relational Analysis, GRA）是一种多因素统计分析方法，它主要用于处理小样本、贫信息不确定性问题。灰色系统理论是基于部分已知信息和部分未知信息的系统，由我国学者邓聚龙教授于1982年提出。灰色关联分析可以用于评估不同序列之间的关联程度，广泛应用于工程、经济、环境科学等多个领域。

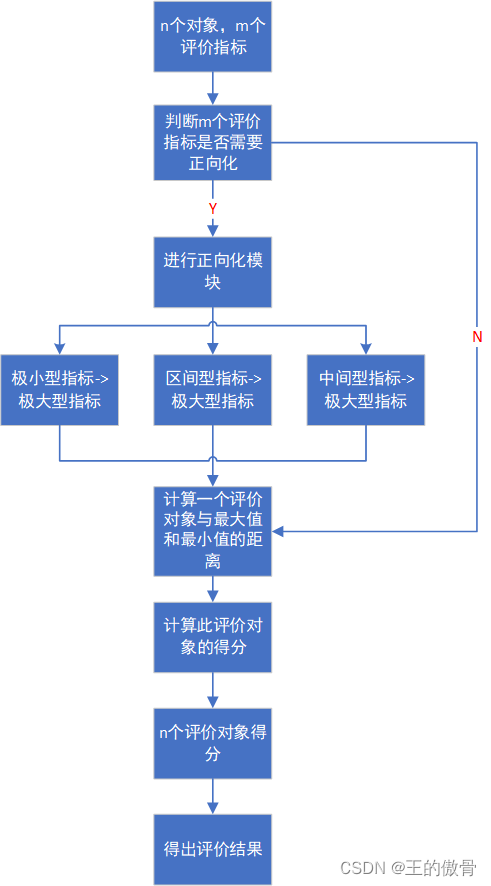
灰色关联分析的基本步骤：

1. 确定比较序列和参考序列：

   • 比较序列是指需要与参考序列进行对比的多个序列。
   • 参考序列是作为标准或目标的序列，通常选择最优或者最差的序列作为参考。

2. 对原始数据进行无量纲化处理：

   • 由于不同指标的数据可能具有不同的量纲（单位），为了消除量纲的影响，需要对原始数据进行无量纲化处理，常用的方法有初值化、均值化等。

3. 计算关联系数：

   • 根据公式计算比较序列中的每个点与参考序列对应点之间的关联系数。关联系数反映了两序列在某一点上的关联程度，其值一般介于0和1之间。

4. 计算关联度：

   • 关联度是对所有时间点上关联系数的一个综合评价，通过加权平均或者其他方式得到。

5. 根据关联度排序：

   • 对比序列按照关联度大小排序，关联度越大说明该序列与参考序列越相似，反之则差异越大。

6. 结果分析：

   • 分析排序结果，得出结论，并据此为决策提供依据。

     

     

     

应用实例：

例如，在评估某个地区经济发展状况时，可以选取GDP、人均收入、工业总产值等若干个经济指标构成比较序列，以全国平均水平或者理想水平作为参考序列，通过灰色关联分析找出哪些因素与经济发展最相关，从而为政策制定提供参考。

灰色关联分析的优点在于它不需要大量的样本数据，也不要求数据服从特定的概率分布，因此对于一些难以获取大量数据的情况非常适用。但是，它的缺点是主观性较强，比如在选择参考序列、权重分配等方面可能会引入人为因素，影响分析结果的客观性。

代码

code1（无需正向化）

%% 灰色关联分析用于系统分析例题的讲解
clear;clc
% A=[55 24 10;65 38 22;75 40 18;100 50 20]
A=input('请输入初始矩阵=')  % 输入初始矩阵
Mean = mean(A);  % 求出每一列的均值以供后续的数据预处理
A = A ./ repmat(Mean,size(A,1),1);  %size(A,1)=6, repmat(Mean,6,1)可以将矩阵进行复制，复制为和A同等大小，然后使用点除（对应元素相除），这些在第一讲层次分析法都讲过
disp('预处理后的矩阵为：'); disp(A)
Y = A(:,1);  % 母序列
X = A(:,2:end); % 子序列
absX0_Xi = abs(X - repmat(Y,1,size(X,2)))  % 计算|X0-Xi|矩阵(在这里我们把X0定义为了Y)
a = min(min(absX0_Xi))    % 计算两级最小差a
b = max(max(absX0_Xi))  % 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi  + rho*b)  % 计算子序列中各个指标与母序列的关联系数
disp('子序列中各个指标的灰色关联度分别为：')
disp(mean(gamma))

code2(要判断是否需要正向化)

clear;clc
%%  1.判断是否需要正向化
% A=[9 10 175 120;8 7 164 80;6 3 157 90]
X=input('指标矩阵A=');    %%输入判断矩阵
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标']) 
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理，需要请输入1 ，不需要输入0：  ']);

if Judge == 1
    Position = input('请输入需要正向化处理的指标所在的列，例如第2、3、6三列需要处理，那么你需要输入[2,3,6]： '); %[2,3,4]
    disp('请输入需要处理的这些列的指标类型（1：极小型， 2：中间型， 3：区间型） ')
    Type = input('例如：第2列是极小型，第3列是区间型，第6列是中间型，就输入[1,3,2]：  '); %[2,1,3]
    % 注意，Position和Type是两个同维度的行向量
    for i = 1 : size(Position,2)  %这里需要对这些列分别处理，因此我们需要知道一共要处理的次数，即
        % 循环的次数
        X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
    % Positivization是我们自己定义的函数，其作用是进行正向化，其一共接收三个参数
    % 第一个参数是要正向化处理的那一列向量 X(:,Position(i))   回顾上一讲的知识，X(:,n)表示取第n列的全部元素
    % 第二个参数是对应的这一列的指标类型（1：极小型， 2：中间型， 3：区间型）
    % 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
    % 该函数有一个返回值，它返回正向化之后的指标，我们可以将其直接赋值给我们原始要处理的那一列向量
    end
    disp('正向化后的矩阵 X = ')
    disp(X)
end

%% 对正向化后的矩阵进行预处理
Mean = mean(X);  % 求出每一列的均值以供后续的数据预处理
Z = X ./ repmat(Mean,size(X,1),1);  
disp('预处理后的矩阵为：'); disp(Z)

%% 构造母序列和子序列
Y = max(Z,[],2);  % 母序列为虚拟的，用每一行的最大值构成的列向量表示母序列
X = Z; % 子序列就是预处理后的数据矩阵

%% 计算得分
absX0_Xi = abs(X - repmat(Y,1,size(X,2)))  % 计算|X0-Xi|矩阵
a = min(min(absX0_Xi))    % 计算两级最小差a
b = max(max(absX0_Xi))  % 计算两级最大差b
rho = 0.5; % 分辨系数取0.5
gamma = (a+rho*b) ./ (absX0_Xi  + rho*b)  % 计算子序列中各个指标与母序列的关联系数
weight = mean(gamma) / sum(mean(gamma));  % 利用子序列中各个指标的灰色关联度计算权重
score = sum(X .* repmat(weight,size(X,1),1),2);   % 未归一化的得分
stand_S = score / sum(score);   % 归一化后的得分
[sorted_S,index] = sort(stand_S ,'descend') % 进行排序

用于正向化的函数

Inter2Max

function [posit_x] = Inter2Max(x,a,b)
    r_x = size(x,1);  % row of x 
    M = max([a-min(x),max(x)-b]);
    posit_x = zeros(r_x,1);   %zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
    % 初始化posit_x全为0  初始化的目的是节省处理时间
    for i = 1: r_x
        if x(i) < a
           posit_x(i) = 1-(a-x(i))/M;
        elseif x(i) > b
           posit_x(i) = 1-(x(i)-b)/M;
        else
           posit_x(i) = 1;
        end
    end
end

Mid2Max

function [posit_x] = Mid2Max(x,best)
    M = max(abs(x-best));
    posit_x = 1 - abs(x-best) / M;
end

Min2Max

function [posit_x] = Min2Max(x)
    posit_x = max(x) - x;
     %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
end

Positivization

% function [输出变量] = 函数名称(输入变量）  
% 函数的中间部分都是函数体
% 函数的最后要用end结尾
% 输出变量和输入变量可以有多个，用逗号隔开
% function [a,b,c]=test(d,e,f)
%     a=d+e;
%     b=e+f;
%     c=f+d;
% end
% 自定义的函数要单独放在一个m文件中，不可以直接放在主函数里面（和其他大多数语言不同）

function [posit_x] = Positivization(x,type,i)
% 输入变量有三个：
% x：需要正向化处理的指标对应的原始列向量
% type： 指标的类型（1：极小型， 2：中间型， 3：区间型）
% i: 正在处理的是原始矩阵中的哪一列
% 输出变量posit_x表示：正向化后的列向量
    if type == 1  %极小型
        disp(['第' num2str(i) '列是极小型，正在正向化'] )
        posit_x = Min2Max(x);  %调用Min2Max函数来正向化
        disp(['第' num2str(i) '列极小型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 2  %中间型
        disp(['第' num2str(i) '列是中间型'] )
        best = input('请输入最佳的那一个值： ');
        posit_x = Mid2Max(x,best);
        disp(['第' num2str(i) '列中间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    elseif type == 3  %区间型
        disp(['第' num2str(i) '列是区间型'] )
        a = input('请输入区间的下界： ');
        b = input('请输入区间的上界： '); 
        posit_x = Inter2Max(x,a,b);
        disp(['第' num2str(i) '列区间型正向化处理完成'] )
        disp('~~~~~~~~~~~~~~~~~~~~分界线~~~~~~~~~~~~~~~~~~~~')
    else
        disp('没有这种类型的指标，请检查Type向量中是否有除了1、2、3之外的其他值')
    end
end