原理

主成分分析法（Principal Component Analysis，PCA）是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性无关的变量，转换后的这组变量叫主成分。在数据科学和机器学习中，PCA常被用来进行降维处理。

PCA的主要目的：

  1. 数据压缩：减少数据集的维度，同时尽量保留原始数据的变异信息。

  2. 去噪：通过去除低方差的成分，可以有效降低数据中的噪声。

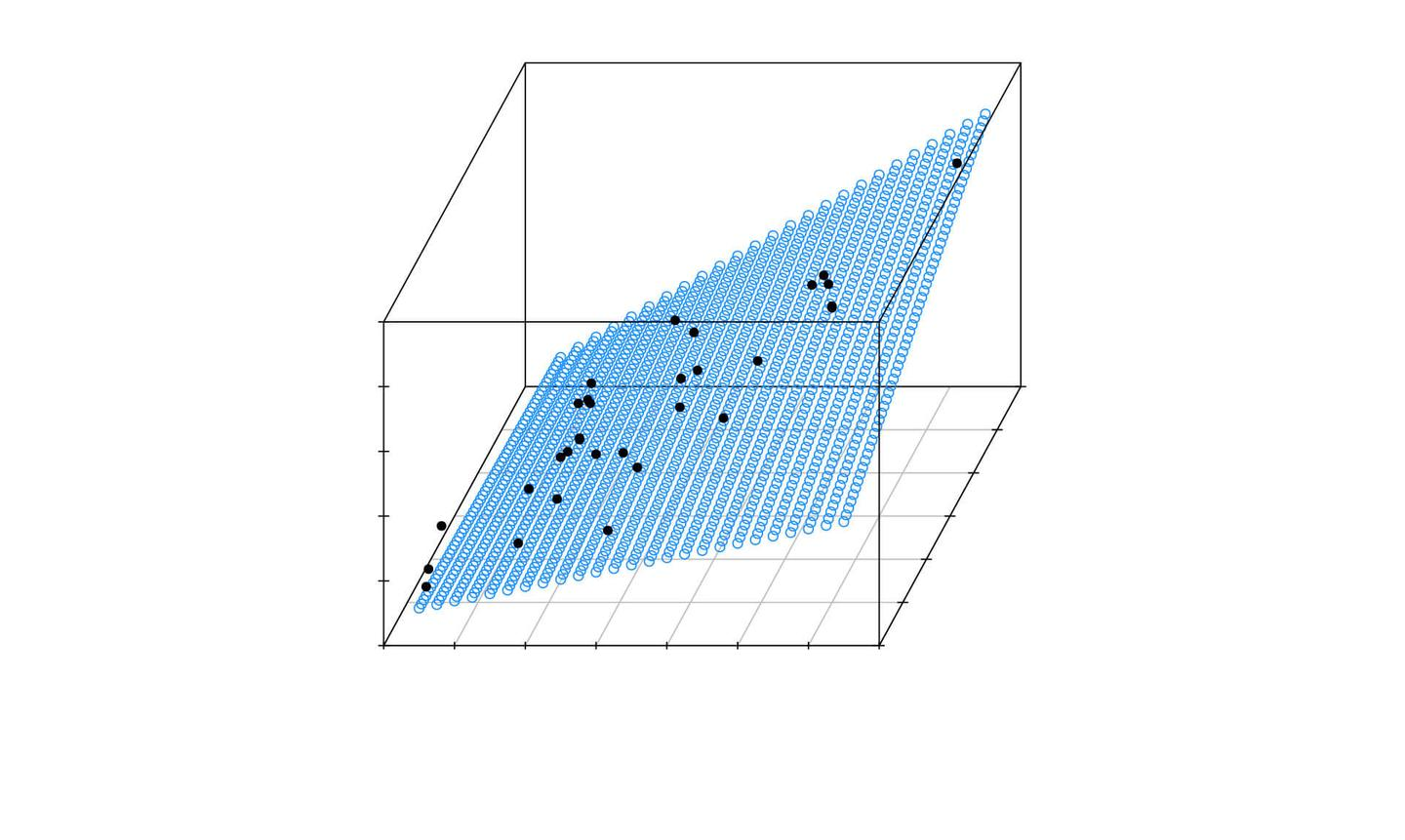
  3. 可视化：将高维数据转换到二维或三维空间中以便于可视化。

    思想：

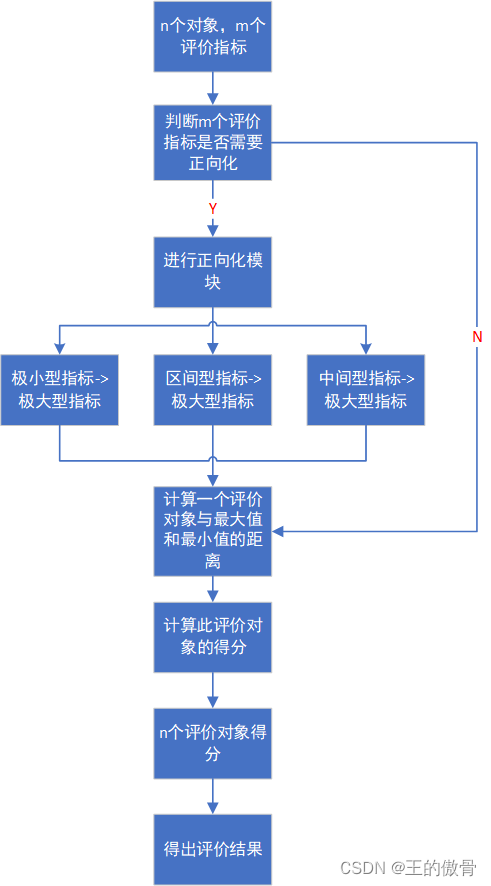
PCA的基本步骤：

  1. 标准化数据：因为PCA对量纲敏感，所以需要对原始数据进行标准化，使得每个特征的均值为0，方差为1。

  2. 计算协方差矩阵：协方差矩阵能表示不同特征之间的关系以及它们的分布情况。

  3. 计算协方差矩阵的特征值和特征向量：特征值表示对应特征向量方向上的数据分散程度。

  4. 选择主成分：根据特征值大小排序，选择最大的几个特征值对应的特征向量作为主成分。这些主成分代表了数据的最大方差方向。

  5. 投影数据：将原始数据投影到由所选主成分构成的新坐标系中，得到降维后的数据。

    计算步骤：

注意事项：

  • PCA假设数据是线性相关的，并且新的成分是原始变量的线性组合。
  • PCA是无监督的学习方法，它并不考虑类别标签信息。
  • 降维后的主成分通常是不可解释的，因为它们是原始特征的线性组合。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
clear;clc
load data1.mat % 加载所用的数据
[n,p] = size(x);  % n是样本个数，p是指标个数

%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)

%% 第二步：计算样本协方差矩阵
R = cov(X);


%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵


%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)