原理

线性规划（Linear Programming, LP）是一种优化技术，用于在满足一系列线性不等式或等式的约束条件下，最大化或最小化一个线性目标函数。线性规划模型通常包含以下几个组成部分：

  1. 决策变量：这些是需要求解的未知数，它们代表了我们希望做出的决策。例如，在生产计划中，决策变量可能是每种产品的生产数量。

  2. 目标函数：这是我们需要优化的表达式，即最大化或最小化的函数。目标函数由决策变量的线性组合构成。例如，最大化利润或最小化成本。

  3. 约束条件：这些是限制决策变量值的线性不等式或等式。它们反映了资源的有限性、技术上的限制或其他实际操作中的要求。例如，原材料的数量、机器的工作时间等。

  4. 非负条件：通常情况下，决策变量不能取负值，因为这在许多实际问题中没有意义。比如，你不能制造负数量的产品。

线性规划问题可以表示为以下标准形式：

  • 最大化或最小化目标函数 Z = c1x1 + c2x2 + ... + cnxn
  • 满足约束条件 a11x1 + a12x2 + ... + a1nxn <= b1
               `a21x1 + a22x2 + ... + a2nxn <= b2`
           ...
           `am1x1 + am2x2 + ... + amnxn <= bm`
  • 并且所有决策变量 xi >= 0

这里，ci 是目标函数中每个变量的系数，aij 是约束条件中每个变量的系数，而 bi 是约束条件的右边常数项。

解决线性规划问题的方法有很多，最常用的是单纯形法（Simplex Method），它是一个迭代过程，从一个可行解开始逐步移动到更好的解，直到找到最优解。此外，还有内点法（Interior Point Methods）、椭球法（Ellipsoid Method）等其他算法。

线性规划被广泛应用于各个领域，如制造业、运输业、金融行业等，用以帮助进行资源配置、成本控制、收益最大化等方面的战略决策。

代码

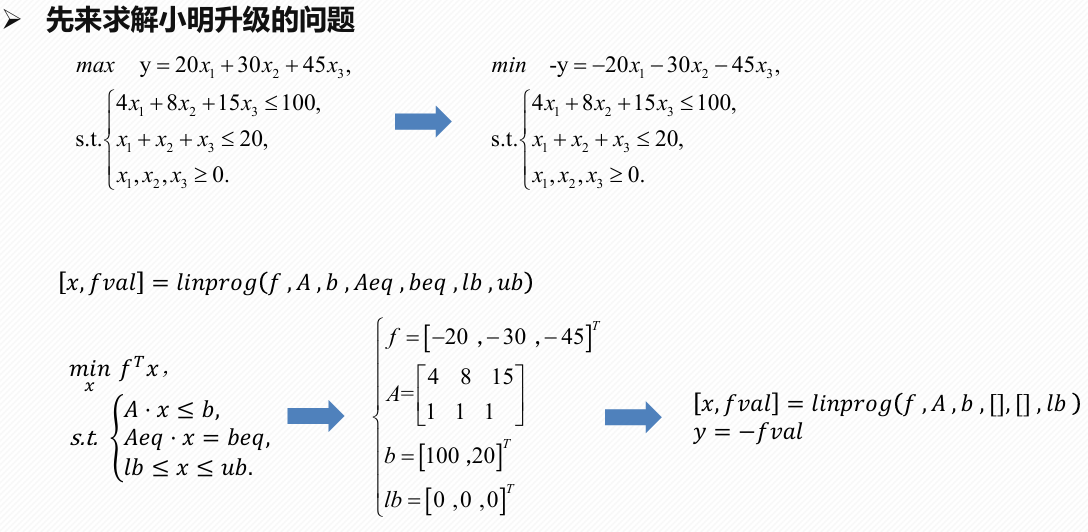
linprog函数：

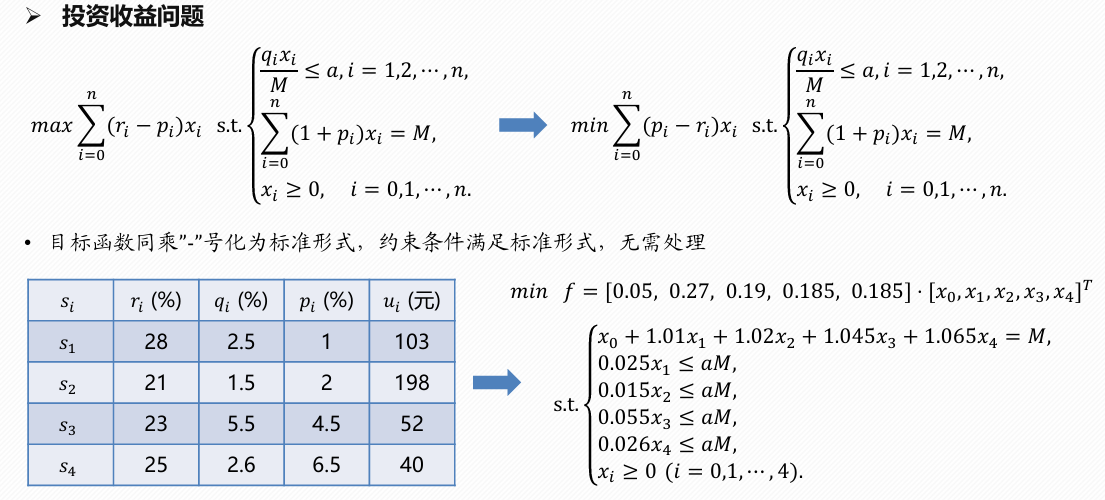
例子：

1
2
3
4
5
6
7
8
9
10
11
clc , clear
f = [-20 ;-30 ;-45]; 
A = [4 ,8 ,15;1 ,1 ,1;]; 
b = [100 ;20];
lb = zeros(3 ,1);
[x,fval] = linprog(f ,A ,b ,[] ,[] ,lb) %没有等号约束
y = -fval  %目标函数为最大化
disp('A、B、C三图分别通关的次数为：')
disp(x)
disp('最终获得的经验为：')
disp(y)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
% clc是清除命令行窗口，clear是清除存储空间的变量
clc,clear;
% a矩阵的元素是不同风险率，从0到0.05等差取值，相邻两个数相差0.001
a = (0:0.001:0.05); % a=[0 0.001 0.002 0.003 0.004 0.005]
f = [-0.05,-0.27,-0.19,-0.185,-0.185];      % 目标函数的系数向量
% A是不等式约束条件的变量系数构成的矩阵
% 用zeros(4,1)先构造4行一列的全是0的矩阵，也就是对x_0无约束；
% 再构造对角矩阵diag([0.025,0.015,0.055,0.026])，对角线上元素为约束条件中变量的系数
A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])];   % 拼接两个矩阵
Aeq = [1,1.01,1.02,1.045,1.065];        % 等式约束的系数矩阵，也就是所有资产投资
beq = 1;
lb = zeros(5,1);
Q = zeros(1,length(a));     % 初始化保存最优解的矩阵Q，因为现在还没求出最优解，元素全设为0
XX = [];    % 定义个空矩阵，用来存不同风险率下的最优解
% 利用矩阵Q存储风险率a(i)下最大的收益；for循环中i在变化，风险率a(i)不同，求出对应的最优解存在矩阵Q内
for i = 1:length(a)         % length求出矩阵a的元素个数，有多少个元素，就循环多少次  
    b = a(i)*ones(4,1);     % b是约束条件的常数项矩阵,4行1列，每个元素值都是常数a(i)
    [x,y] = linprog(f,A,b,Aeq,beq,lb);      % 调用linprog函数
    Q(i) = -y;      % 负负得正，就是所需求的最大值了
    XX = [XX;x'];
end
plot(a,Q,'*r');      % 以风险率为横轴，收益为纵轴，绘制不同风险率下的最优收益
xlabel('风险率');        % x和y轴分别附上标签
ylabel('最大收益');