原理

整数规划（Integer Programming, IP）和0-1规划（Binary or Zero-One Programming）是运筹学中线性规划的两个特殊类型，它们在优化问题中用于寻找最优解。这类问题的特点是在决策变量上增加了整数或二进制（0或1）的约束条件。

整数规划

整数规划是指在优化模型中，部分或全部决策变量被要求取整数值的问题。这与普通的线性规划不同，在线性规划中，决策变量可以取任何实数值。整数规划的一个重要子类是纯整数规划（Pure Integer Programming），其中所有决策变量都必须取整数值；而混合整数规划（Mixed Integer Programming, MIP）则允许某些变量取实数值，其他变量取整数值。

整数规划的应用非常广泛，例如项目选择、生产计划、网络设计等。由于整数约束的存在，整数规划问题往往比相应的线性规划问题更难求解，因为它们通常不是凸优化问题，并且可能具有多个局部最优解。

0-1规划

0-1规划是整数规划的一种特殊情况，其中决策变量仅限于取值0或1。这意味着每个变量只能表示“是”或“否”的选择。0-1规划也被称为二进制规划（Binary Programming）。

0-1规划特别适用于需要做出二元选择的情况，如是否投资一个项目、是否选择一条路径、是否分配一项任务等。由于其离散性质，0-1规划问题通常采用分支定界法（Branch and Bound）、切割平面法（Cutting Plane Method）或启发式算法来求解。

解决方法

对于这两种类型的规划问题，常用的方法包括但不限于：

  • 分支定界法：通过系统地分割问题空间并为每个子问题计算界限，逐步缩小可行解范围。
  • 切割平面法：向原问题添加额外的约束（称为切割平面）以去除非整数解，直到找到整数解为止。
  • 动态规划：适合解决特定结构的整数规划问题。
  • 启发式和元启发式算法：如遗传算法、模拟退火、禁忌搜索等，这些方法不保证找到全局最优解，但可以在合理的时间内找到满意解。

整数规划和0-1规划在实际应用中非常重要，尤其是在涉及资源分配、组合优化等领域。由于这些问题往往是NP难问题，即随着问题规模增大，计算复杂度会急剧增加，因此研究者们不断探索新的算法和技术以提高求解效率。

代码

背包问题

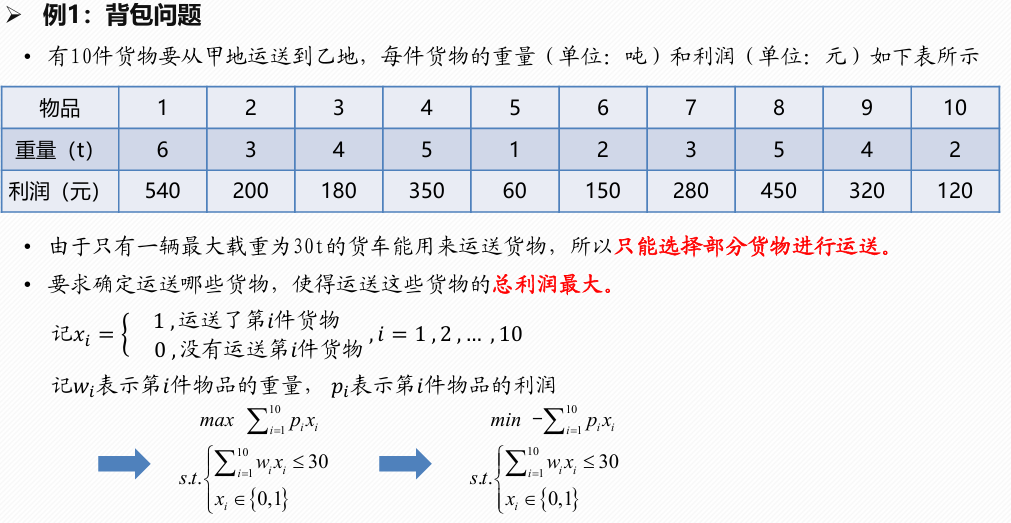
1
2
3
4
5
6
7
8
9
10
%% 背包问题（货车运送货物的问题）
c = -[540 200 180 350 60 150 280 450 320 120];  % 目标函数的系数矩阵(最大化问题记得加负号)
intcon=[1:10];  % 整数变量的位置(一共10个决策变量，均为0-1整数变量)
A = [6 3 4 5 1 2 3 5 4 2];  b = 30;   % 线性不等式约束的系数矩阵和常数项向量（物品的重量不能超过30）
Aeq = []; beq =[];  % 不存在线性等式约束
lb = zeros(10,1);  % 约束变量的范围下限
ub = ones(10,1);  % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
fval = -fval

指派问题

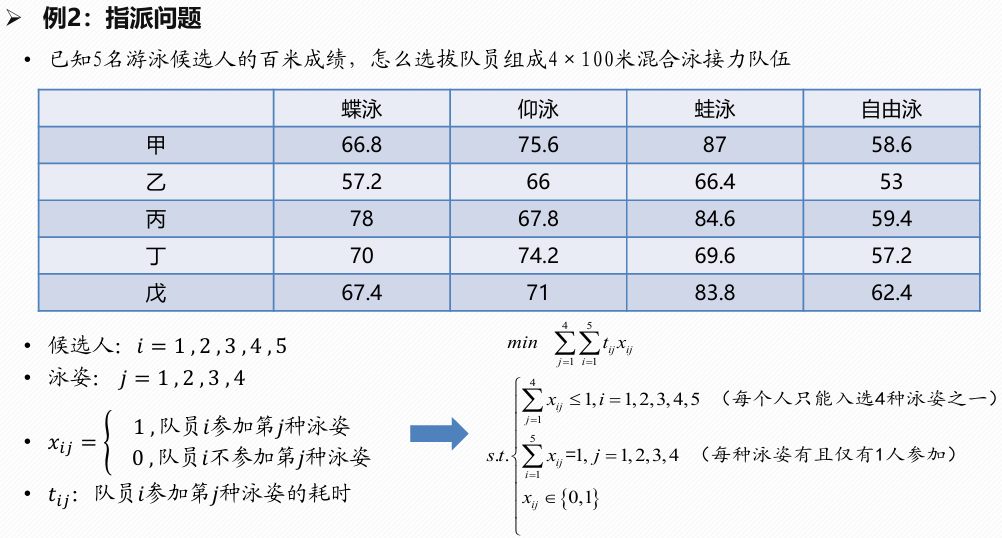
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
A%% 指派问题（选择队员去进行游泳接力比赛）
clear;clc
% 双下标要转换为单下标：x11→x1，x12→x2，…，x24→x8，…，x54→x20
c = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]';  
% 目标函数的系数矩阵（先列后行的写法）
intcon = [1:20];  % 整数变量的位置(一共20个决策变量，均为0-1整数变量)
% 线性不等式约束的系数矩阵和常数项向量（每个人只能入选四种泳姿之一，一共五个约束）
A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
% A = zeros(5,20);
% for i = 1:5
%     A(i, (4*i-3): 4*i) = 1;
% end
b = [1;1;1;1;1];
% 线性等式约束的系数矩阵和常数项向量 （每种泳姿有且仅有一人参加，一共四个约束）
Aeq = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;
       0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;
       0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;
       0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)];  % 或者写成 repmat(eye(4),1,5)  
beq = [1;1;1;1];
lb = zeros(20,1);  % 约束变量的范围下限
ub = ones(20,1);  % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
% reshape(x,4,5)'
%      0     0     0     1    甲自由泳
%      1     0     0     0    乙蝶泳
%      0     1     0     0    丙仰泳
%      0     0     1     0    丁蛙泳
%      0     0     0     0    戊不参加

游戏升级

1
2
3
4
5
6
7
8
9
10
11
12
clc , clear
f = [-20 ;-30 ;-40]; 
intcon=[1:3]
A = [4 ,8 ,10;1 ,1 ,1;]; 
b = [100 ;20];
lb = zeros(3 ,1);
[x,fval] = intlinprog(f ,intcon, A ,b ,[] ,[] ,lb) %没有等号约束
y = -fval  %目标函数为最大化
disp('A、B、C三图分别通关的次数为：')
disp(x)
disp('最终获得的经验为：')
disp(y)