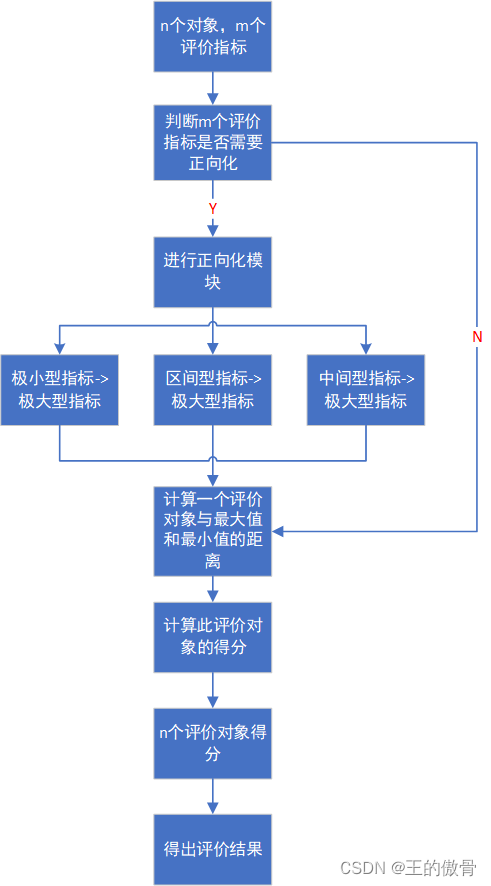
最小最大化模型

原理

最小最大化模型（Minimax Model），是优化领域中的一种建模方法，主要用于决策制定过程中处理不确定性或对抗性环境。这类模型试图找到一种策略，使得最坏情况下的结果尽可能好。

Maximin 模型

在maximin模型中，目标是选择一个策略，以确保即使是在最不利的情况下，也能获得尽可能好的结果。换句话说，就是从所有可能的最差结果中选取最好的一个。这种模型常用于保守决策者希望最小化其潜在损失的情境中。

应用例子：

• 投资组合选择：投资者可能会使用maximin模型来选择投资组合，以保证即使市场表现最糟糕时，他们也能获得一定的回报。
• 军事战略：指挥官可能采用maximin模型来规划战术，确保即便面对敌方的最佳反击，己方仍能维持最低限度的成功。

Minimax 模型

相反，在minimax模型中，目标是寻找一种策略，使最坏情况下的损失最小化。这通常用于博弈论和对抗环境中，其中一方试图预测并对抗另一方的最佳反应。minimax模型特别适用于两人零和游戏，其中一个玩家的收益直接等于另一个玩家的损失。

应用例子：

• 国际象棋等游戏中的人工智能算法：AI会尝试通过minimax搜索树来预测对手的最优行动，并据此作出回应，以最小化自己的最大可能损失。
• 经济政策制定：政府可能利用minimax模型来设计经济政策，以应对最严重的经济衰退情景。

应用场景

最大最小化模型广泛应用于多个领域：

• 风险管理：企业可以通过考虑最坏情况下的影响来进行风险评估和管理。
• 供应链管理：制造商可以使用这些模型来优化库存水平，确保即使在需求波动或供应中断的情况下也能保持运营连续性。
• 资源分配：公共部门或非营利组织可以使用maximin/minimax原则来公平地分配有限资源，确保每个受益群体至少得到一定水平的支持。

解决方法

解决maximin/minimax问题的方法取决于具体的应用背景和数学形式。常见的求解技术包括线性规划、动态规划、整数规划等。对于复杂的非线性或离散问题，还可能需要使用启发式算法或元启发式算法，如遗传算法、粒子群优化等。

总之，maximin和minimax模型提供了处理不确定性和对抗性情境的有效框架，帮助决策者在复杂多变的环境中做出稳健的选择。

代码

选址问题

Fun.m

function f = Fun(x)
    a=[1 4 3 5 9 12 6 20 17 8];
    b=[2 10 8 18 1 4 5 10 8 9];
    %  函数向量
    f=zeros(10,1);
    for i = 1:10
        f(i) = abs(x(1)-a(i))+abs(x(2)-b(i));  
    end
% f(1) = abs(x(1)-a(1))+abs(x(2)-b(1));  
% f(2) = abs(x(1)-a(2))+abs(x(2)-b(2));
% f(3) = abs(x(1)-a(3))+abs(x(2)-b(3));
% f(4) = abs(x(1)-a(4))+abs(x(2)-b(4));
% f(5) = abs(x(1)-a(5))+abs(x(2)-b(5));
% f(6) = abs(x(1)-a(6))+abs(x(2)-b(6));
% f(7) = abs(x(1)-a(7))+abs(x(2)-b(7));
% f(8) = abs(x(1)-a(8))+abs(x(2)-b(8));
% f(9) = abs(x(1)-a(9))+abs(x(2)-b(9));
% f(10) = abs(x(1)-a(10))+abs(x(2)-b(10));
end 

maxmin.m

%% 最大最小化模型  :   min{max[f1,f2,···,fm]}
x0 = [6, 6];      % 给定初始值
lb = [3, 4];  % 决策变量的下界
ub = [8, 10];  % 决策变量的上界
[x,feval] = fminimax(@Fun,x0,[],[],[],[],lb,ub)
max(feval)
% x =
%     8.0000    8.5000
% feval =
%    13.5000    5.5000    5.5000   12.5000    8.5000    8.5000    5.5000   13.5000    9.5000    0.5000
% 结论：
% 在坐标为(8,8.5)处建立供应中心可以使该点到各需求点的最大距离最小，最小的最大距离为13.5单位。