一元线性回归分析模型
原理
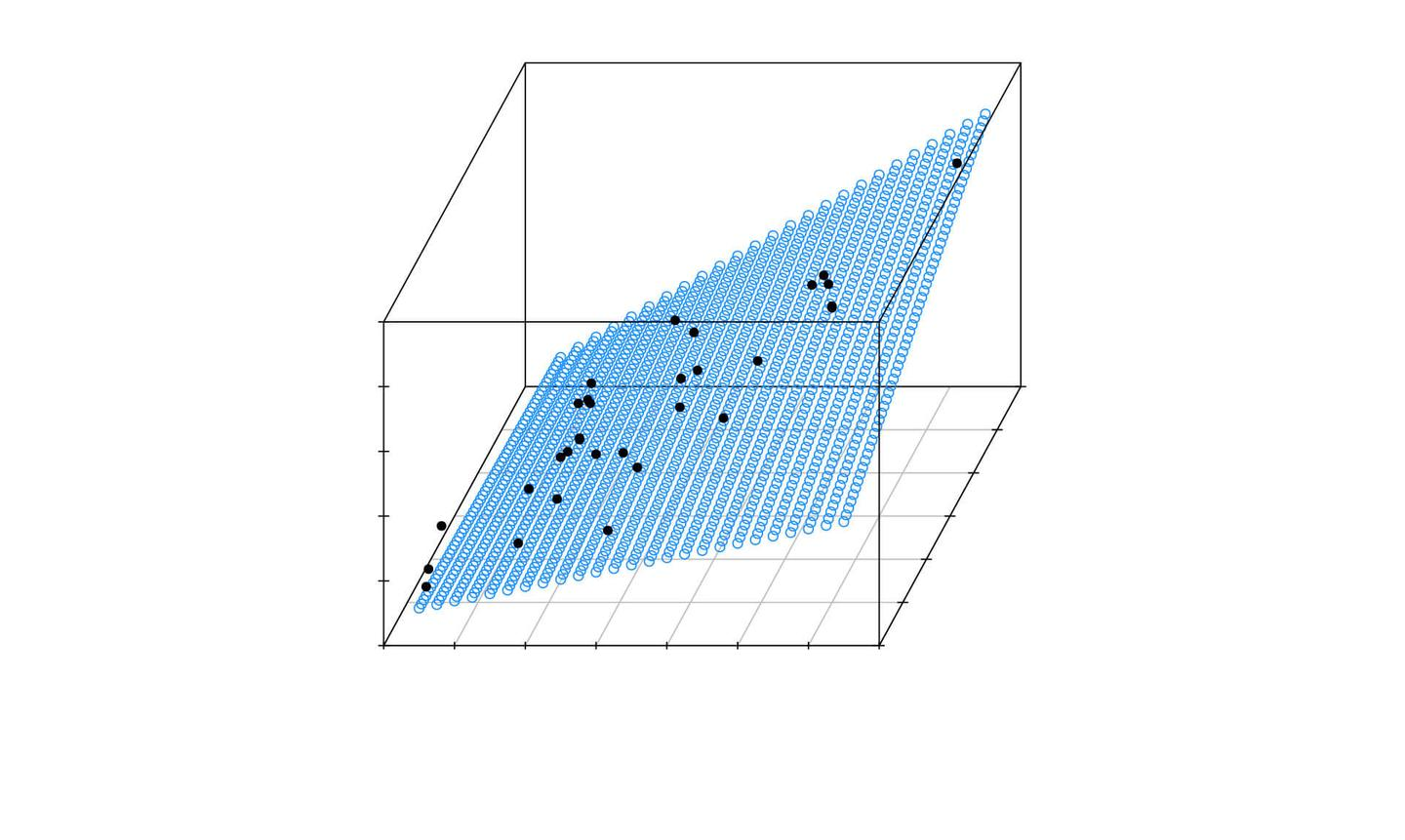
一元线性回归分析模型(Simple Linear Regression Model)是一种统计方法,用于研究两个连续变量之间的关系:一个因变量(通常记为 (Y))和一个自变量(通常记为 (X))。这个模型假设这两个变量之间存在线性关系,并试图通过最小化预测值与实际观测值之间的差异来拟合一条直线。

残差图作图命令:rcoplot(r,rint)



建模步骤
- 数据收集:首先需要收集包含因变量和自变量的数据集。
- 模型设定:设定一元线性回归模型的形式,即 (Y = \beta_0 + \beta_1 X + \epsilon)。
- 参数估计:使用最小二乘法(Ordinary Least Squares, OLS)等方法来估计未知参数 (\beta_0) 和 (\beta_1)。OLS的目标是找到使残差平方和最小化的参数值,即 (\sum (Y_i - (\beta_0 + \beta_1 X_i))^2) 最小。
- 模型评估:评估模型的好坏,包括检查模型的拟合优度(如R²)、进行假设检验(如t检验和F检验)以确定参数是否显著不为零,以及检查残差图来验证模型假设(如误差项的正态性和同方差性)。
- 预测:一旦模型被验证为合理且有效,就可以用它来进行预测,即对于给定的 (X) 值,预测相应的 (Y) 值。
注意事项
- 确保数据满足线性关系的前提条件。
- 检查是否存在异常点或强影响点,它们可能会对回归系数产生不成比例的影响。
- 确认不存在多重共线性问题,在一元回归中这不是问题,但在多元回归中这是一个重要的考虑因素。
- 验证误差项的独立性和同方差性,以及它们是否服从正态分布。
一元线性回归是更复杂的回归分析(如多元线性回归、非线性回归等)的基础。它是理解和学习更多高级统计技术和机器学习算法的良好起点。
代码
1 | % 1、输入数据 |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Lee的学习之旅!