原理
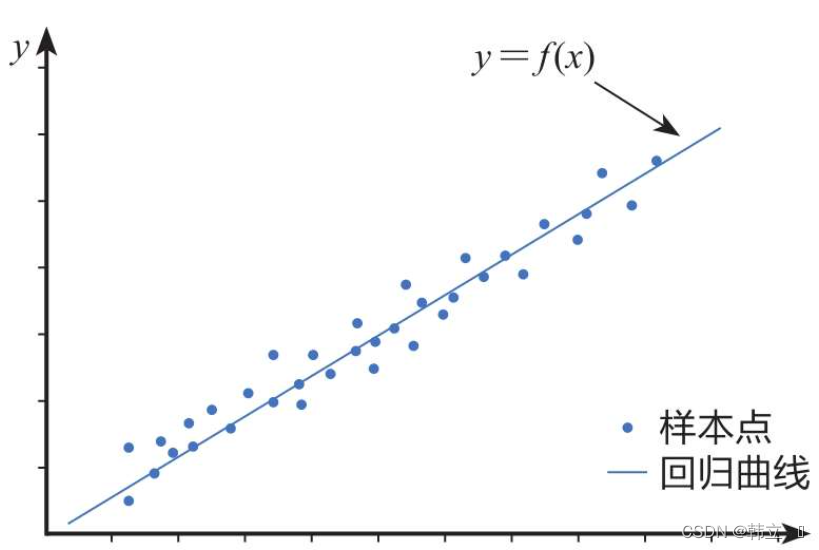
多元线性回归分析是一种统计方法,用于研究一个因变量(也称为响应变量或目标变量)与两个或多个自变量(也称为预测变量或解释变量)之间的关系。其目的是通过最小化预测值与实际观测值之间的差异来拟合一个最佳的线性方程,从而能够根据自变量的值预测因变量的平均值。
为了建立和评估多元线性回归模型,通常需要进行以下步骤:
数据收集:获取包含因变量和自变量的数据集。
模型假设检查:确保满足线性回归的基本假设,包括线性关系、独立性、同方差性和正态性等。
参数估计:使用最小二乘法或其他估计方法来确定模型参数(即截距和斜率)。
模型检验:通过F检验、t检验等统计测试来评估模型的整体显著性和单个预测变量的重要性。
残差分析:检查残差(预测值与实际值之差)以确保它们是随机分布的,并且符合回归分析的假设条件。
模型诊断:识别异常值、高杠杆点和影响点,并考虑是否需要调整模型。
预测和解释:利用模型进行预测,并解释各个自变量对因变量的影响。
模型简化:如果存在不显著的预测变量,可以考虑移除它们以简化模型。
模型验证:在新数据上测试模型的表现,以确认其泛化能力。
多元线性回归广泛应用于经济学、社会学、心理学、医学等多个领域,用于理解不同因素如何共同作用于特定的结果。在应用此方法时,重要的是要保证数据的质量,并仔细解读结果,因为模型只能反映数据中存在的关联,而不是因果关系。





代码
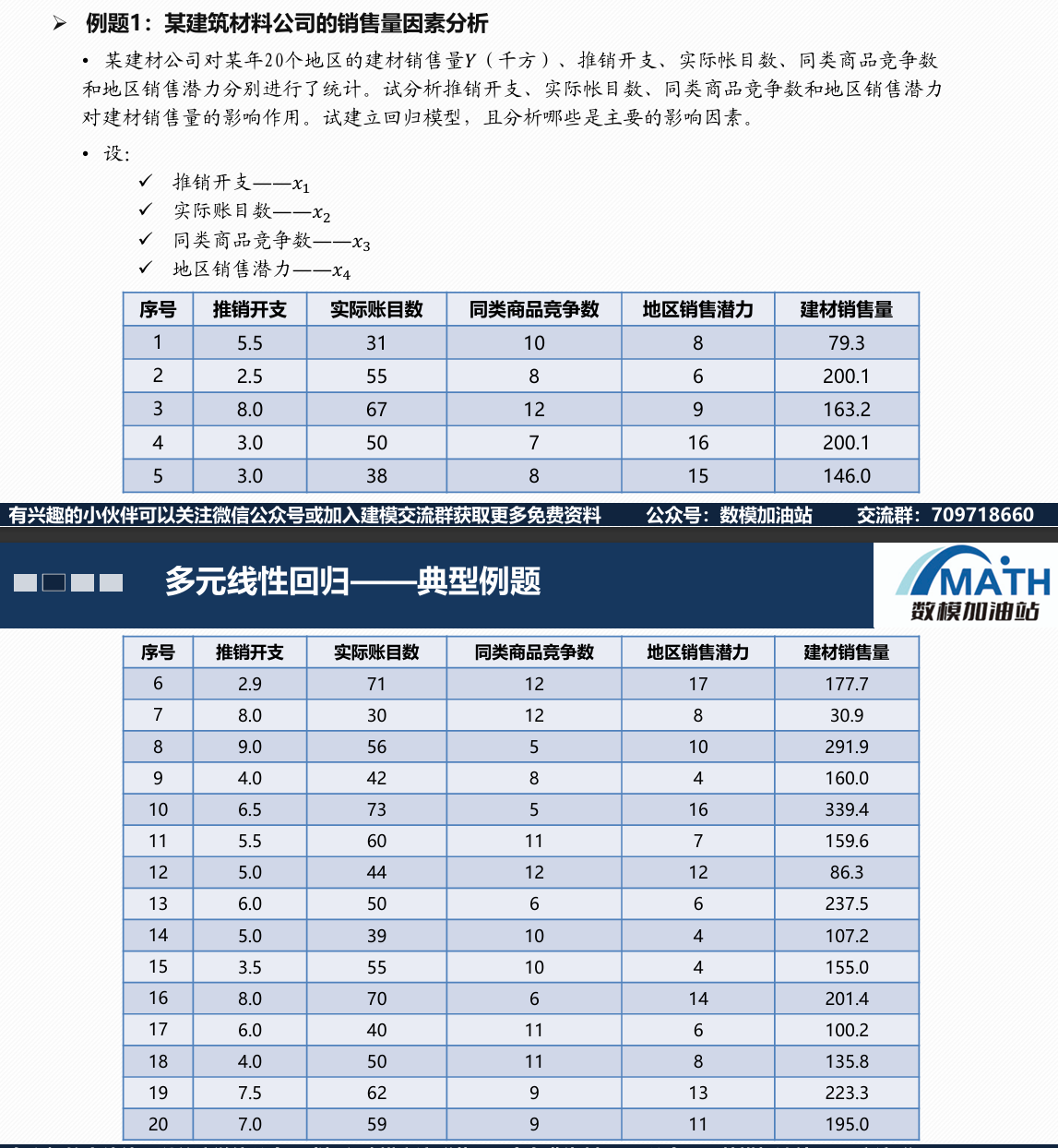
建筑材料公司的销售量因素分析
1
2
3
4
5
6
7
8
9
10
11
12
|
x1=[5.5 2.5 8.0 3.0 3.0 2.9 8.0 9.0 4.0 6.5 5.5 5.0 6.0 5.0 3.5 8.0 6.0 4.0 7.5 7.0]';
x2=[31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 70 40 50 62 59]';
x3=[10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9]';
x4=[8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11]';
y=[79.3 200.1 163.2 200.1 146.0 177.7 30.9 291.9 160.0 339.4 159.6 86.3 237.5 107.2 155.0 201.4 100.2 135.8 223.3 195.0]';
X=[ones(size(x1)),x1,x2,x3,x4];
[b,bint,r,rint,stats]=regress(y,X)
rcoplot(r,rint)
|
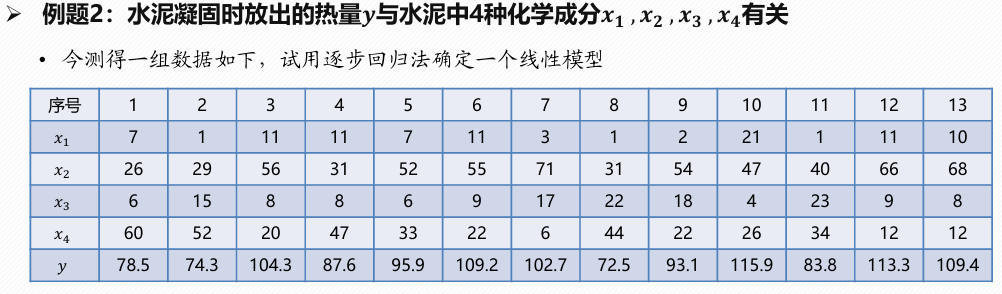
水泥凝固时放热分析
1
2
3
4
5
6
7
8
9
10
|
x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';
x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';
x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';
x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';
y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]';
x=[x1 x2 x3 x4];
stepwise(x,y)
|
作图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
x1 = -10:0.1:10;
x2 = -10:0.1:10;
[X1, X2] = meshgrid(x1, x2);
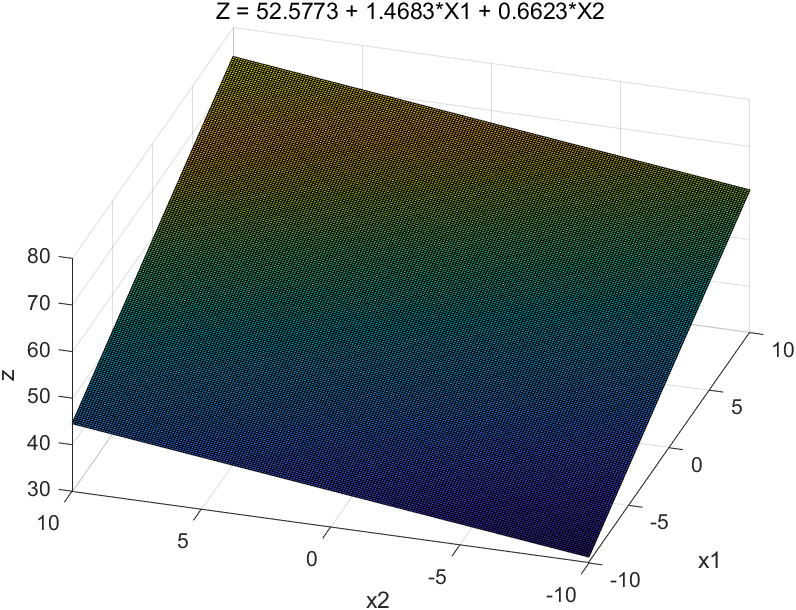
Z = 52.5773 + 1.4683*X1 + 0.6623*X2;
figure;
surf(X1, X2, Z);
xlabel('x1');
ylabel('x2');
zlabel('z');
title('Z = 52.5773 + 1.4683*X1 + 0.6623*X2');
|