多目标规划模型

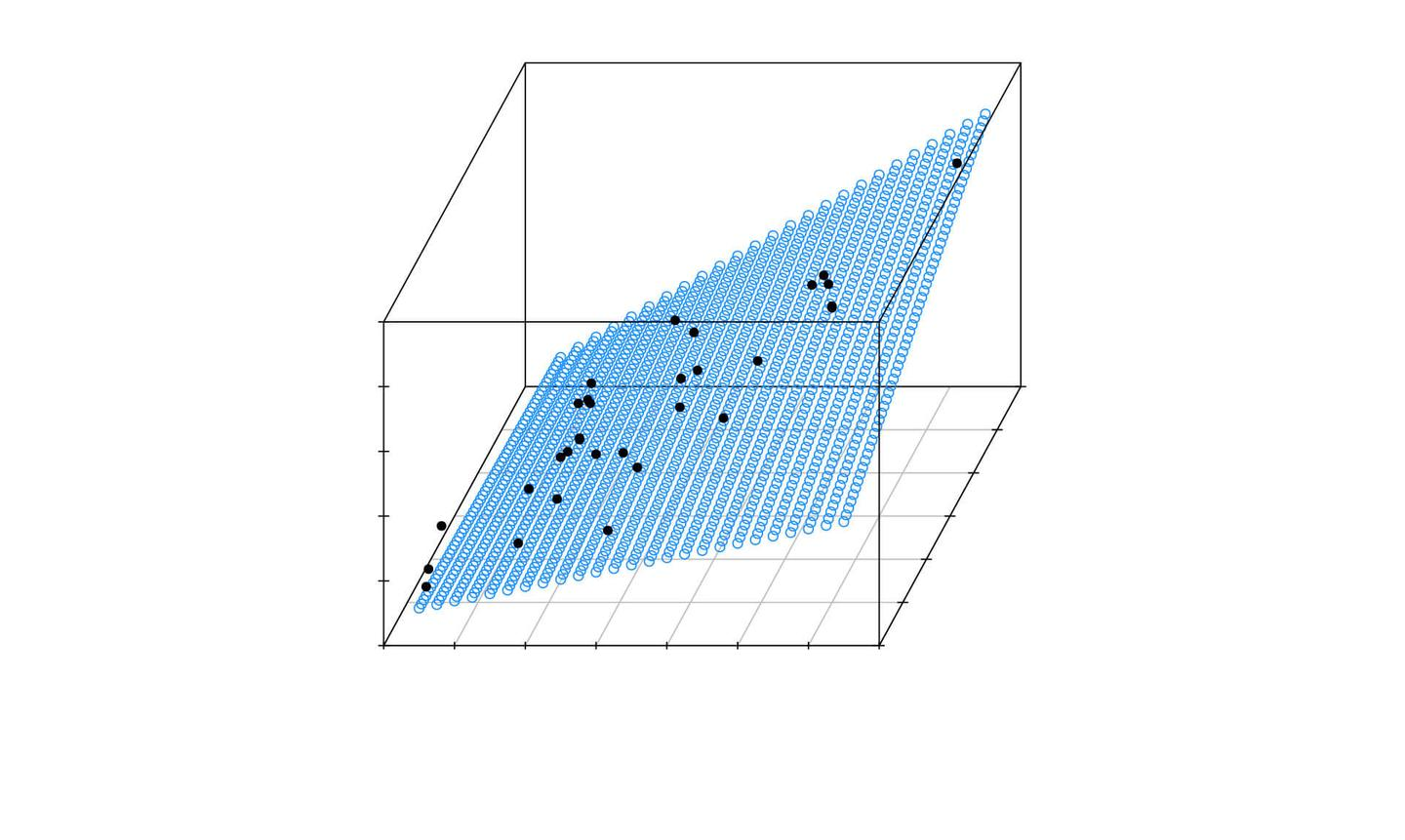
原理

多目标规划模型是一种数学建模方法，它允许决策者同时优化多个目标函数。在现实世界的问题中，通常会遇到需要同时考虑多个不同且常常相互冲突的目标的情况。例如，在一个企业资源分配问题中，可能希望最大化利润的同时最小化成本和环境影响。

解决多目标规划问题的方法有很多，包括但不限于：

1. 加权和法：将所有目标通过赋予不同的权重组合成一个单一的目标函数进行优化。
2. ε-约束法：选择一个目标作为主要目标进行优化，而其他目标则被转化为约束条件。
3. 帕累托最优解集：寻找不是由任何其他解决方案支配的解，即帕累托前沿上的点。
4. 进化算法：如遗传算法、粒子群优化等，它们可以用来近似找到帕累托最优解。
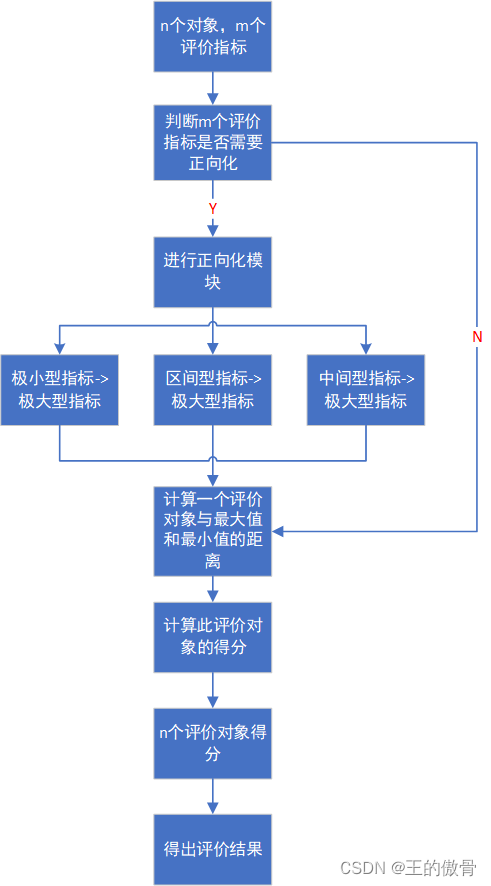
5. 妥协规划：通过定义理想点和计算每个可行解与理想点的距离来找到最佳折衷解。

每种方法都有其适用场景和局限性，选择哪种方法取决于具体问题的特点以及决策者的偏好。

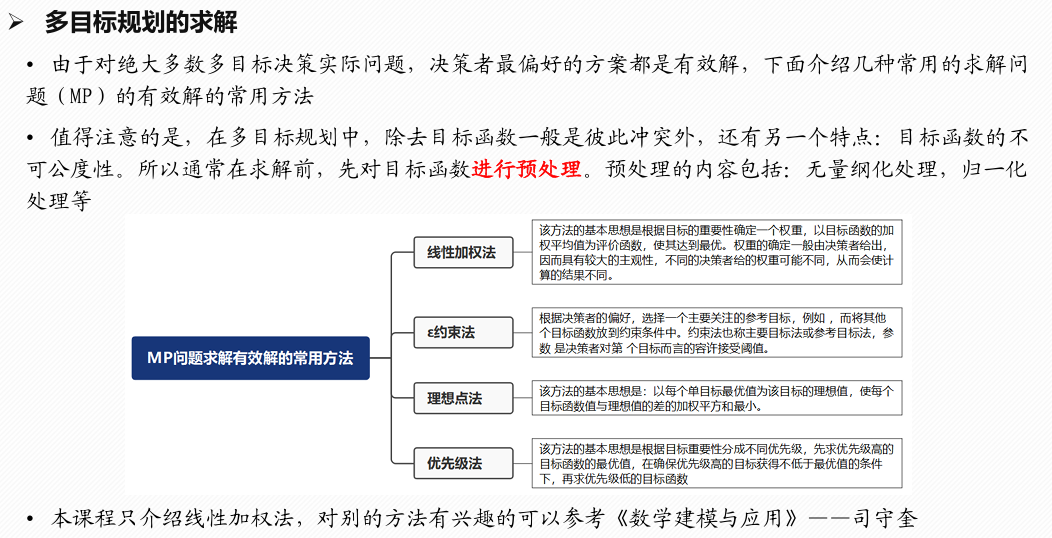
代码

多目标规划问题

w1 = 0.4;  w2 = 0.6;  % 两个目标函数的权重  x1 = 5  x2 = 2
w1 = 0.5;  w2 = 0.5;  % 两个目标函数的权重  x1 = 5  x2 = 2
w1 = 0.3;  w2 = 0.7;  % 两个目标函数的权重  x1 = 1  x2 = 6
c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3];  % 线性规划目标函数的系数
A = [-1 -1];  b = -7; % 不等式约束
lb = [0 0]'; ub = [5 6]'; % 上下界
[x,fval] = linprog(c,A,b,[],[],lb,ub)
f1 = 2*x(1)+5*x(2)
f2 = 0.4*x(1) + 0.3*x(2)

敏感性分析

clear;clc
W1 = 0.1:0.001:0.5;  W2 = 1- W1;  
n =length(W1);
F1 = zeros(n,1);  F2 = zeros(n,1);   X1 = zeros(n,1);  X2 = zeros(n,1);   FVAL = zeros(n,1);
A = [-1 -1];  b = -7; % 不等式约束
lb = [0 0]; ub = [5 6]; % 上下界
for i = 1:n
    w1 = W1(i);  w2 = W2(i);
    c = [w1/30*2+w2/2*0.4 ;w1/30*5+w2/2*0.3];  % 线性规划目标函数的系数
    [x,fval] = linprog(c,A,b,[],[],lb,ub);
    F1(i) = 2*x(1)+5*x(2);
    F2(i) = 0.4*x(1) + 0.3*x(2);
    X1(i) = x(1);
    X2(i) = x(2);
    FVAL(i) = fval;
end

% 在图上可以加上数据游标，按住Alt加鼠标左键可以设置多个数据游标出来。
figure(1) 
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重') 
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')

figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重') 
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')

figure(3)
plot(W1,FVAL)  % 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重') 
ylabel('综合指标的值')