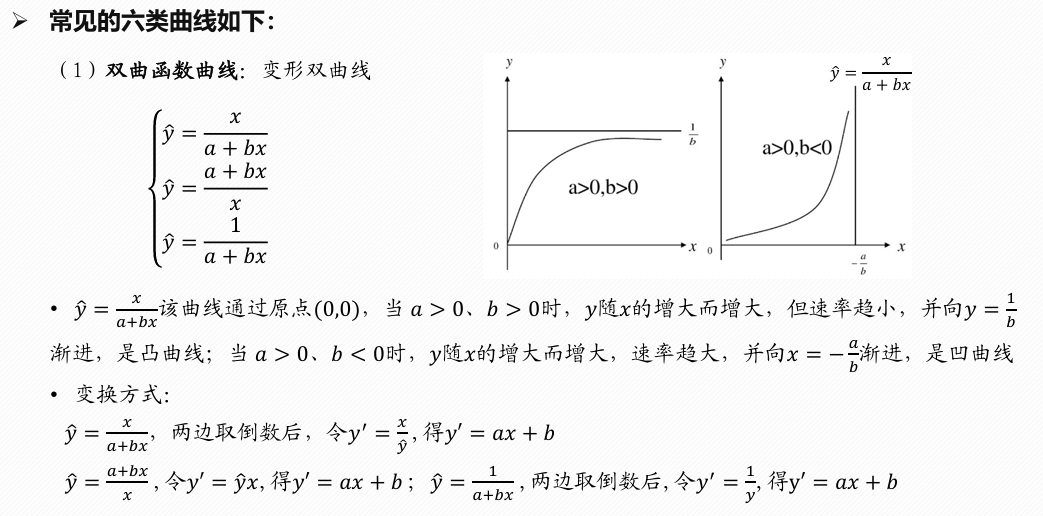
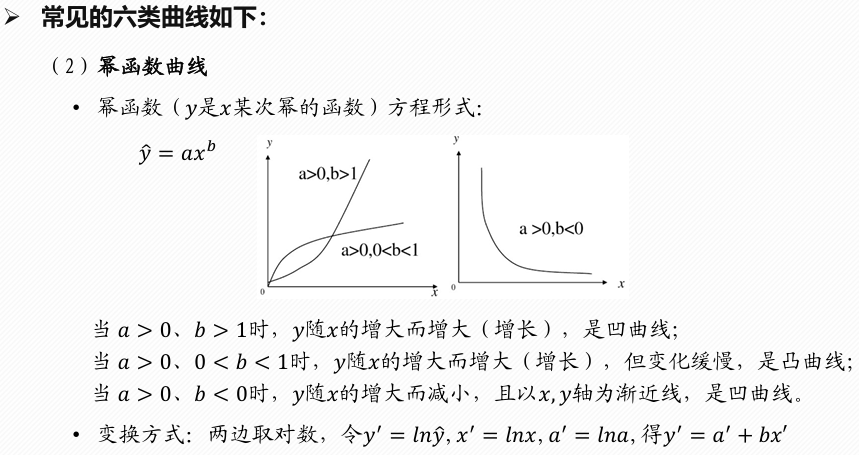
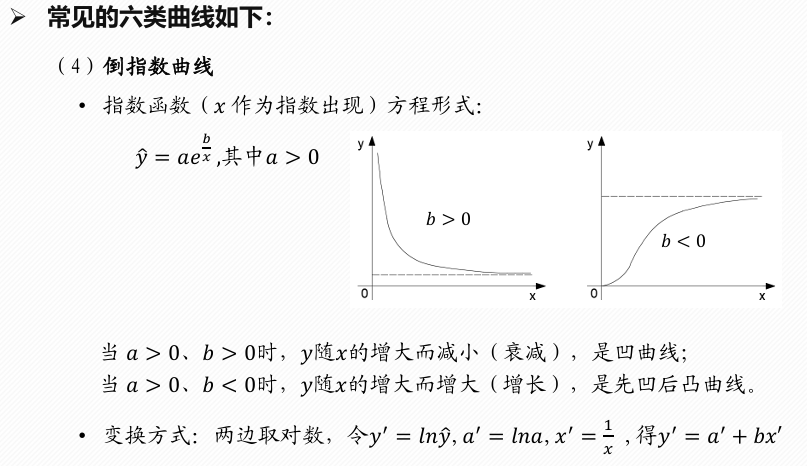
原理

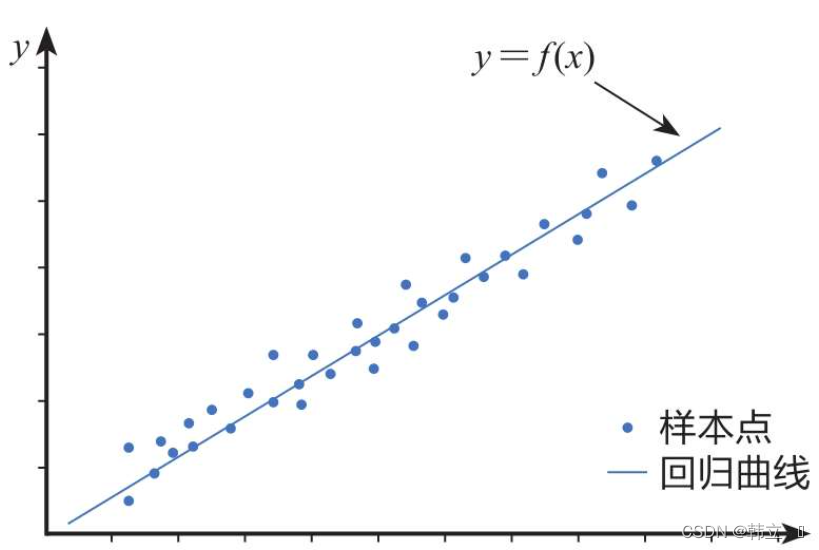
非线性回归分析是一种统计方法，用于研究因变量（响应变量）与一个或多个自变量之间的关系，当这种关系不是线性的而是曲线型时。在非线性回归中，因变量和自变量之间的关系通过一个非线性的函数来表达。这不同于多元线性回归，后者假设因变量是自变量的线性组合。

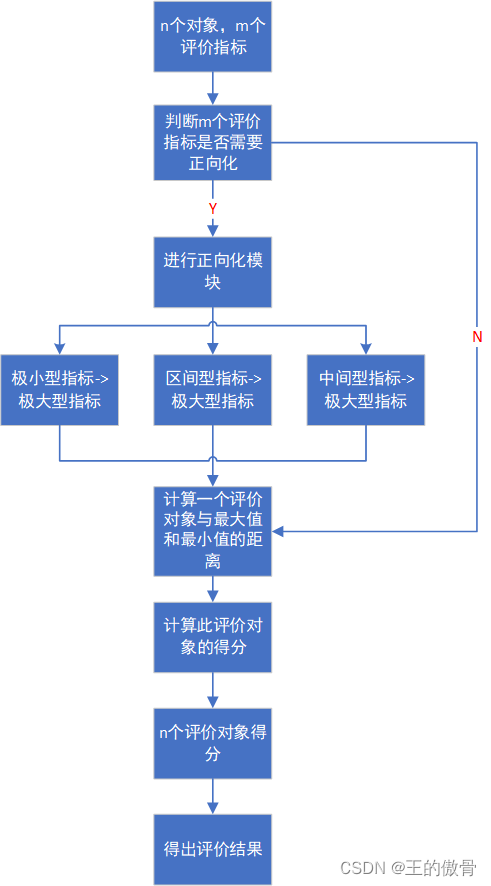
建立非线性回归模型的过程包括以下步骤：

  1. 选择模型：根据理论、经验或者数据探索选择适当的非线性函数形式。
  2. 参数估计：使用迭代算法（如高斯-牛顿法、Levenberg-Marquardt算法等）来寻找最佳拟合参数 ββ，使得预测值与实际观测值之间的差异最小化。
  3. 模型评估：检查模型的拟合优度，例如通过R平方、调整后的R平方、AIC（Akaike信息准则）、BIC（贝叶斯信息准则）等指标，并进行残差分析确保满足回归的基本假设。
  4. 假设检验：对模型参数进行显著性检验，以确定哪些自变量对于解释因变量是重要的。
  5. 诊断与验证：识别异常点、影响点以及可能存在的多重共线性问题；在独立的数据集上验证模型的泛化能力。
  6. 预测：利用最终模型对未来或未知数据的因变量进行预测。

非线性回归的应用非常广泛，从生物学中的生长曲线到经济学中的收益函数都可以用它来建模。由于非线性模型往往比线性模型更复杂，因此需要更多的计算资源和专业知识来进行准确的参数估计和模型评估。此外，非线性回归的结果解释也可能更加困难，因为系数不再具有直接的加成效应。

在实践中，如果怀疑存在非线性关系但不确定具体形式，可以考虑多项式回归作为简单的非线性扩展，或者是采用广义加性模型（GAMs），它们允许每个自变量对因变量有非线性的影响，而不需要指定具体的数学形式。

代码

volum.m

1
2
function yhat=volum(beta,x)
   yhat=beta(1)*exp(beta(2)./x);

code3.m

1
2
3
4
5
6
7
8
9
10
11
12
% 1）输入数据
x=2:16;
y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];
beta0=[8 2]'; %设定初始值，根据经验选择
% 2）求回归系数
[beta,r,J]=nlinfit(x',y','volum',beta0); 
% 使用非线性最小二乘法进行回归拟合，'volum'为定义曲线函数的函数名
beta  % 回归系数

%3）预测及作图
[YY,delta]=nlpredci('volum',x',beta,r,J); % 预测因变量的值及置信区间
plot(x,y,'k+',x,YY,'r')   % 绘制原始数据点和拟合曲线

code2.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
% 1、直接用多元二项式回归
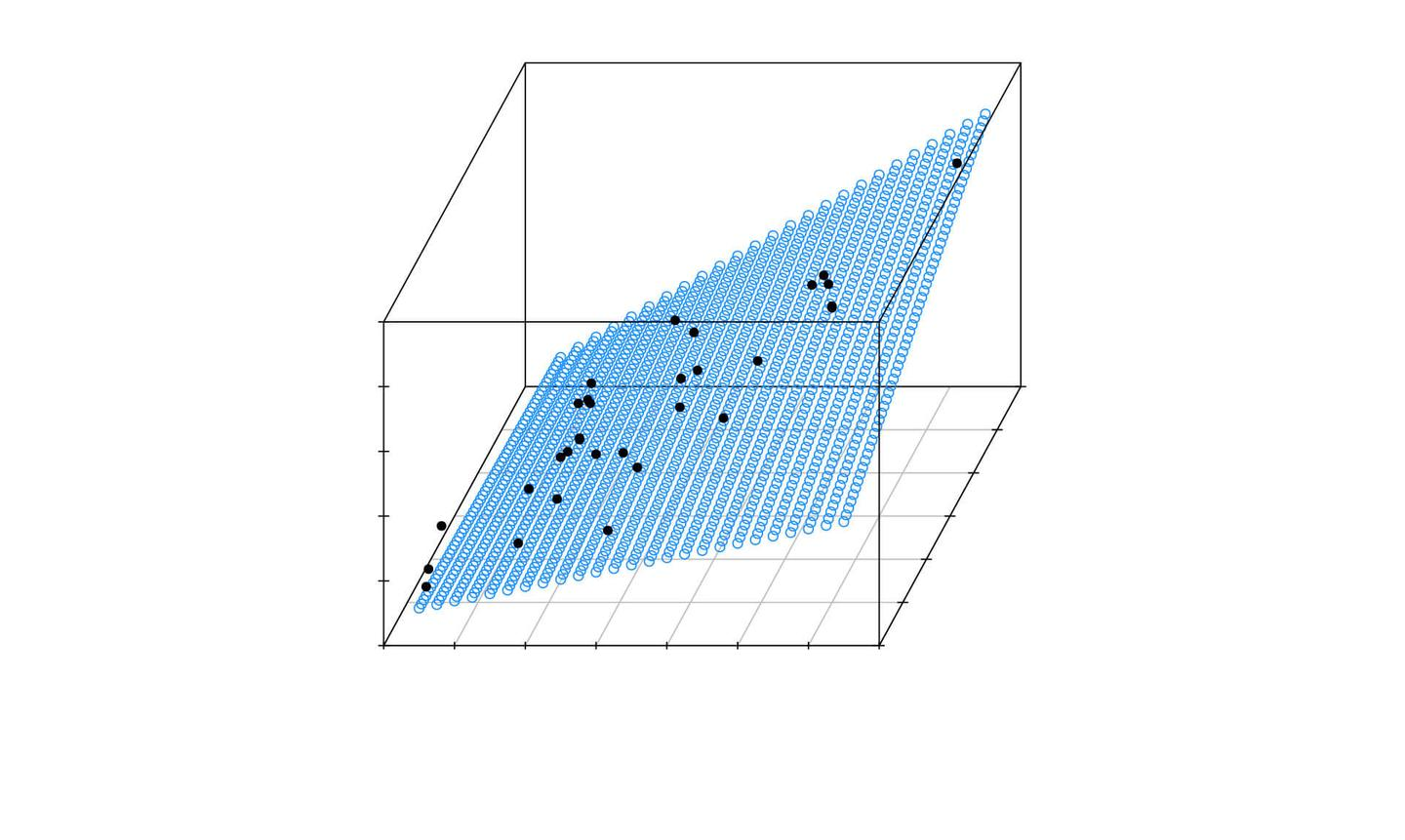
x1=[1000 600 1200 500 300 400 1300 1100 1300 300] ;
x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]';
x=[x1'  x2' ];
rstool(x ,y,'purequadratic')  % 使用多元二项式回归工具箱进行回归分析
beta, rmse  % 回归系数和剩余标准差
% beta=110.5313   0.1464   -26.5709   -0.0001   1.8475 
% rmse=4.5362
% 故回归模型为：𝑦=110.5313+0.1464𝑥_1−26.5709𝑥_2−0.0001𝑥_1^2+1.8475𝑥_2^2
% 剩余标准差仅为4.5362，说明此回归模型的预测效果较好

% 2、化为多元线性回归
% 令x3=x1^2   x4=x2^2
X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)']; % 多元线性回归的自变量矩阵
[b,bint,r,rint,stats]=regress(y,X); % 进行多元线性回归分析
b,stats  % b为回归系数，stats为统计信息
% 结果为：
% b=110.5313     0.1464    -26.5709   -0.0001    1.8475
% stats=0.9702   40.6656   0.0005

code1.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
% 1、二次多项式回归
t = 1/30:1/30:14/30;  % 自变量 t
s = [11.86 15.67 20.6 26.69 33.71 41.93 51.13 61.49 72.9 85.44 99.08 113.77 129.54 146.48];  % 因变量 s
[p, S] = polyfit(t, s, 2);  % 进行二次多项式拟合

% 预测及作图
Y = polyconf(p, t, S);  % 计算拟合曲线的预测值
plot(t, s, 'k+', t, Y, 'r');  % 绘制原始数据点和拟合曲线
xlabel('t');  % 设置 x 轴标签
ylabel('s');  % 设置 y 轴标签
title('二次多项式回归');  % 设置图表标题
legend('原始数据', '拟合曲线');  % 设置图例

% 2、化为多元线性回归
t = 1/30:1/30:14/30;  % 自变量 t
s = [11.86 15.67 20.6 26.69 33.71 41.93 51.13 61.49 72.9 85.44 99.08 113.77 129.54 146.48];  % 因变量 s
% 令x1=t, x2=t^2
T = [ones(14, 1), t', (t.^2)'];  % 构建多元线性回归的自变量矩阵
[b, bint, r, rint, stats] = regress(s', T);  % 进行多元线性回归分析