第2章 算法效率分析基础
2.2 渐进符号和基本效率类型




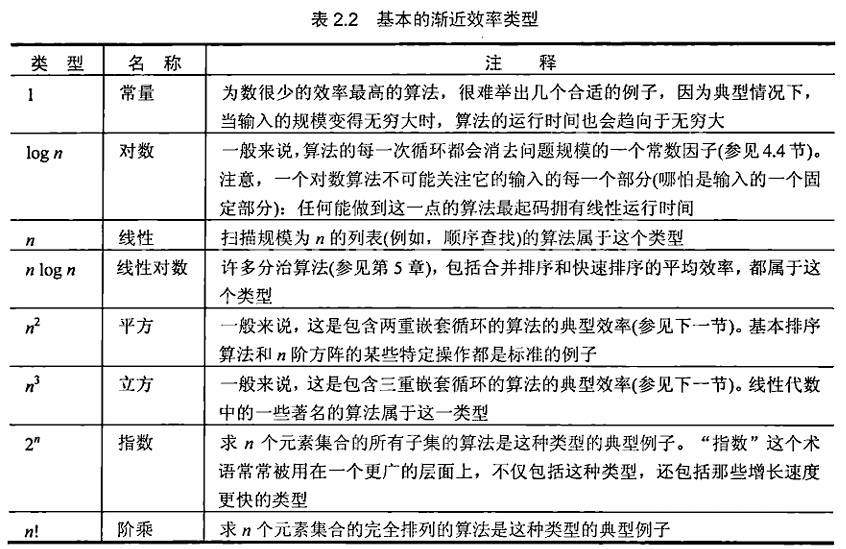
类型按照增长次数的升序排列
2.4 递归算法的数学分析
反向替代法

分析递归算法时间效率的通用方案

汉诺塔游戏
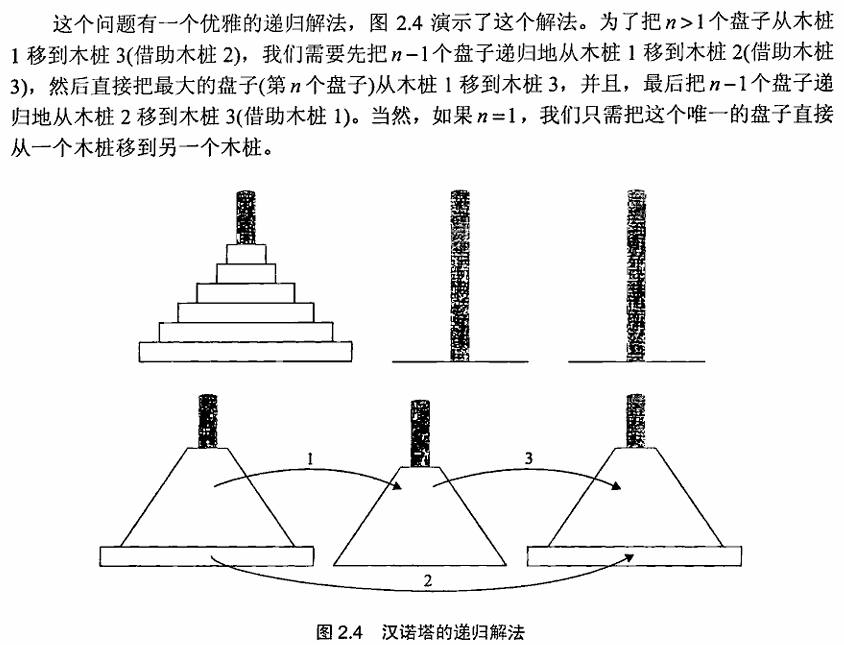
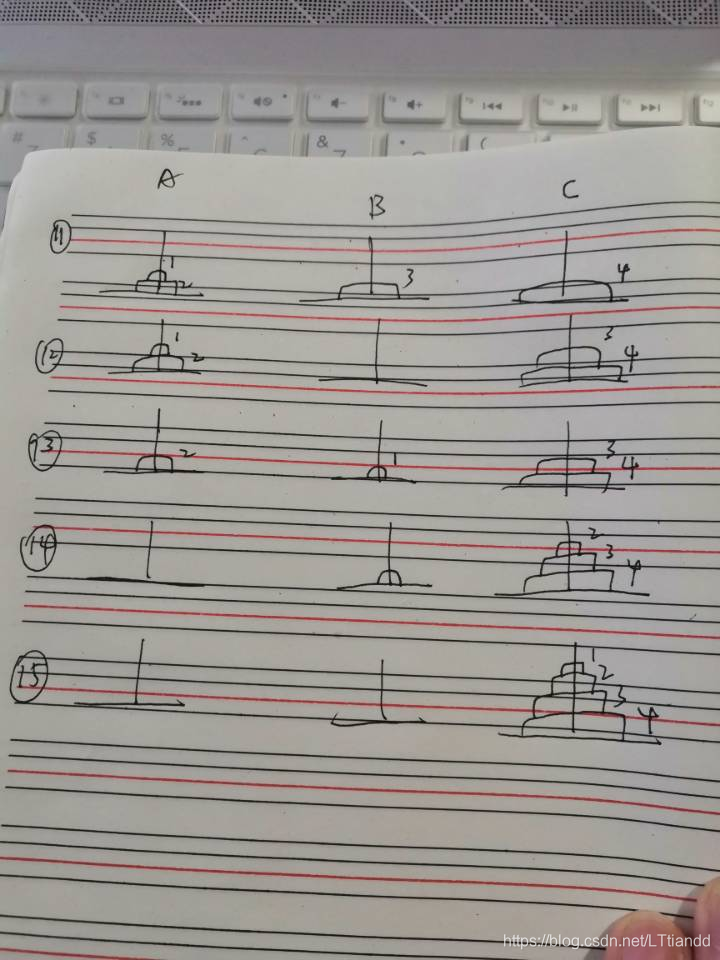
手写的详细步骤
四个盘子时:

代码实现
1 |
|
递推式求解

2.5 例题:计算第n个斐波那契数
初始条件:F[0]=0,F[1]=1
方法一:
1 | int F(int n) |
方法二:
1 | int Fib(int n) |
方法三:


方法四:
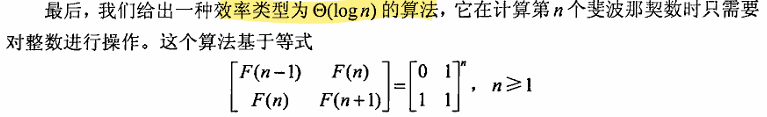
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Lee的学习之旅!