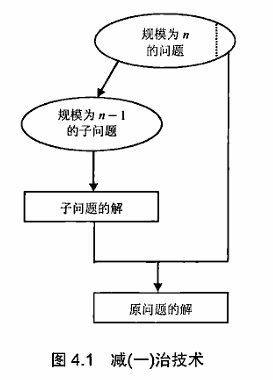
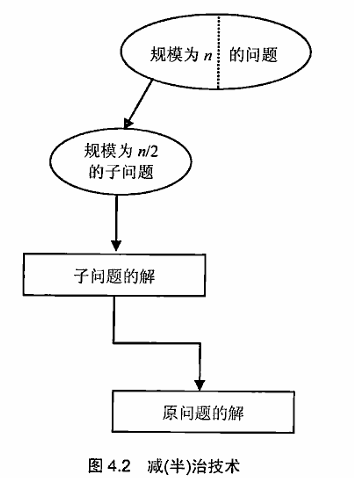
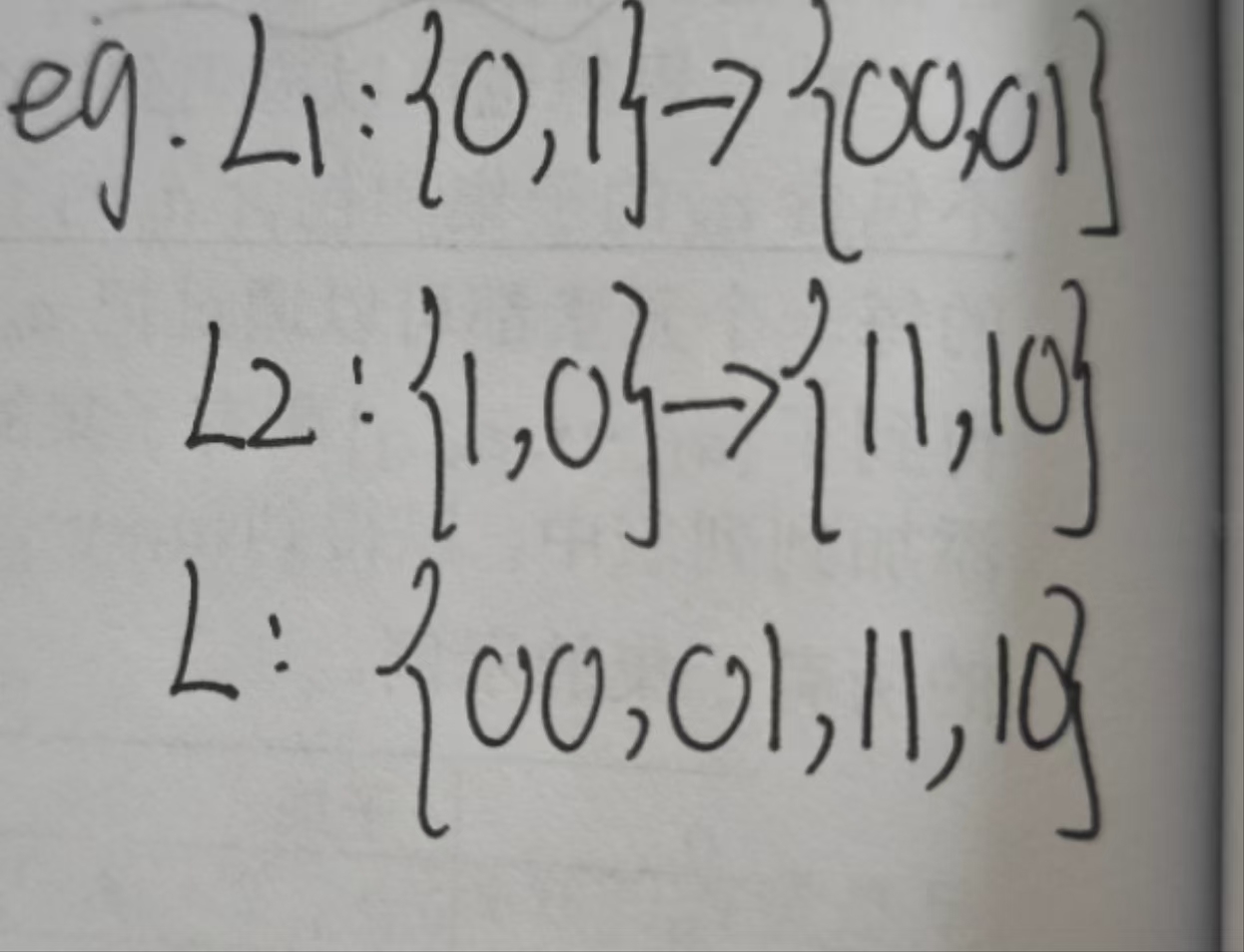4.1 插入排序 插排的代码可看数据结构 中排序那部分
4.3 生成组合对象的算法 Johnson-Trotter算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <iostream> #include <vector> bool canMove (const std::vector<int >& perm, const std::vector<int >& dir, int index) int d = dir[index]; if (d == -1 && index > 0 && perm[index] > perm[index - 1 ]) { return true ; } if (d == 1 && index < perm.size () - 1 && perm[index] > perm[index + 1 ]) { return true ; } return false ; } int findMaxMovable (const std::vector<int >& perm, const std::vector<int >& dir) int max = -1 ; int maxIndex = -1 ; for (int i = 0 ; i < perm.size (); ++i) { if (canMove (perm, dir, i) && perm[i] > max) { max = perm[i]; maxIndex = i; } } return maxIndex; } void reverseLargerDirections (std::vector<int >& dir, const std::vector<int >& perm, int max) for (int i = 0 ; i < perm.size (); ++i) { if (perm[i] > max) { dir[i] = -dir[i]; } } } bool nextPermutation (std::vector<int >& perm, std::vector<int >& dir) int maxIndex = findMaxMovable (perm, dir); if (maxIndex == -1 ) { return false ; } int d = dir[maxIndex]; std::swap (perm[maxIndex], perm[maxIndex + d]); std::swap (dir[maxIndex], dir[maxIndex + d]); reverseLargerDirections (dir, perm, perm[maxIndex + d]); return true ; } void printPermutation (const std::vector<int >& perm) for (int num : perm) { std::cout << num; } std::cout << std::endl; } void johnsonTrotter (int n) std::vector<int > perm (n) ; std::vector<int > dir (n, -1 ) ; for (int i = 0 ; i < n; ++i) { perm[i] = i + 1 ; } do { printPermutation (perm); } while (nextPermutation (perm, dir)); } int main () int n = 3 ; johnsonTrotter (n); return 0 ; }
n=3时的输出结果:
LexicographicPermute算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <iostream> #include <vector> #include <algorithm> bool nextLexicographicPermutation (std::vector<int >& perm) int n = perm.size (); int i = n - 2 ; while (i >= 0 && perm[i] >= perm[i + 1 ]) { i--; } if (i < 0 ) { return false ; } int j = n - 1 ; while (perm[j] <= perm[i]) { j--; } std::swap (perm[i], perm[j]); std::reverse (perm.begin () + i + 1 , perm.end ()); return true ; } void printPermutation (const std::vector<int >& perm) for (int num : perm) { std::cout << num; } std::cout << std::endl; } void lexicographicPermute (int n) std::vector<int > perm (n) ; for (int i = 0 ; i < n; ++i) { perm[i] = i + 1 ; } do { printPermutation (perm); } while (nextLexicographicPermutation (perm)); } int main () int n = 3 ; lexicographicPermute (n); return 0 ; }
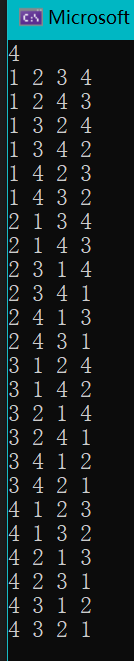
n=4时的输出结果:
二进制反射格雷码生成子集
递归实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class GrayCode {public : vector<string> getGray (int n) { int m = pow (2 ,n); vector<string>str (m); if (n<1 )return {}; if (1 ==n){ str[0 ]="0" ; str[1 ]="1" ; return str; } vector<string>pre_gray = getGray (n-1 ); for (int i=0 ;i<pre_gray.size ();i++){ str[i]="0" + pre_gray[i]; str[m-1 -i]="1" + pre_gray[i]; } return str; } };
非递归实现:
1 2 3 4 5 6 7 vector<int > grayCode (int n) { vector<int >res; for (int i=0 ;i<(1 <<n);i++){ res.push_back (i^(i>>1 )); } return res; }
n=2时:
HeapPermute算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <iostream> #include <vector> void printPermutation (const std::vector<int >& perm) for (int num : perm) { std::cout << num; } std::cout << std::endl; } void heapPermute (std::vector<int >& perm, int size) if (size == 1 ) { printPermutation (perm); return ; } for (int i = 0 ; i < size; ++i) { heapPermute (perm, size - 1 ); if (size % 2 == 1 ) { std::swap (perm[0 ], perm[size - 1 ]); } else { std::swap (perm[i], perm[size - 1 ]); } } } int main () int n = 3 ; std::vector<int > perm (n) ; for (int i = 0 ; i < n; ++i) { perm[i] = i + 1 ; } heapPermute (perm, n); return 0 ; }
递归实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 #include <iostream> #include <cstring> #include <algorithm> using namespace std;const int N = 10 ;int n;int st[N];bool used[N];void dfs (int u) if (u>n) { for (int i=1 ;i<=n;i++) { printf ("%d " ,st[i]); } puts ("" ); return ; } for (int i=1 ;i<=n;i++) { if (!used[i]) { st[u]=i; used[i]=true ; dfs (u+1 ); used[i]=false ; st[u]=0 ; } } } int main () cin >> n; dfs (1 ); return 0 ; }
4.4 减常因子算法 折半查找:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int binary_search (int arr[], int n, int x) int left = 0 , right = n - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (arr[mid] == x) return mid; if (arr[mid] < x) left = mid + 1 ; else right = mid - 1 ; } return -1 ; }
4.5 减可变规模算法 选择问题(selection problem) 是求一个n个数列表的第k个最小元素的问题。
quickselect算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 #include <iostream> #include <vector> #include <algorithm> int partition (std::vector<int >& arr, int left, int right) int pivot = arr[right]; int i = left - 1 ; for (int j = left; j < right; ++j) { if (arr[j] <= pivot) { ++i; std::swap (arr[i], arr[j]); } } std::swap (arr[i + 1 ], arr[right]); return i + 1 ; } int quickselect (std::vector<int >& arr, int left, int right, int k) if (left == right) { return arr[left]; } int pivotIndex = partition (arr, left, right); int rank = pivotIndex - left + 1 ; if (k == rank) { return arr[pivotIndex]; } else if (k < rank) { return quickselect (arr, left, pivotIndex - 1 , k); } else { return quickselect (arr, pivotIndex + 1 , right, k - rank); } } int findKthSmallest (std::vector<int >& arr, int k) if (k < 1 || k > arr.size ()) { throw std::invalid_argument ("k 超出有效范围" ); } return quickselect (arr, 0 , arr.size () - 1 , k); } int main () std::vector<int > arr = {3 , 1 , 4 , 1 , 5 , 9 , 2 , 6 , 5 , 3 , 5 }; int k = 3 ; try { int kthSmallest = findKthSmallest (arr, k); std::cout << "第 " << k << " 小的元素是: " << kthSmallest << std::endl; } catch (const std::invalid_argument& e) { std::cerr << "错误: " << e.what () << std::endl; } return 0 ; }
quickselect的一个例子: