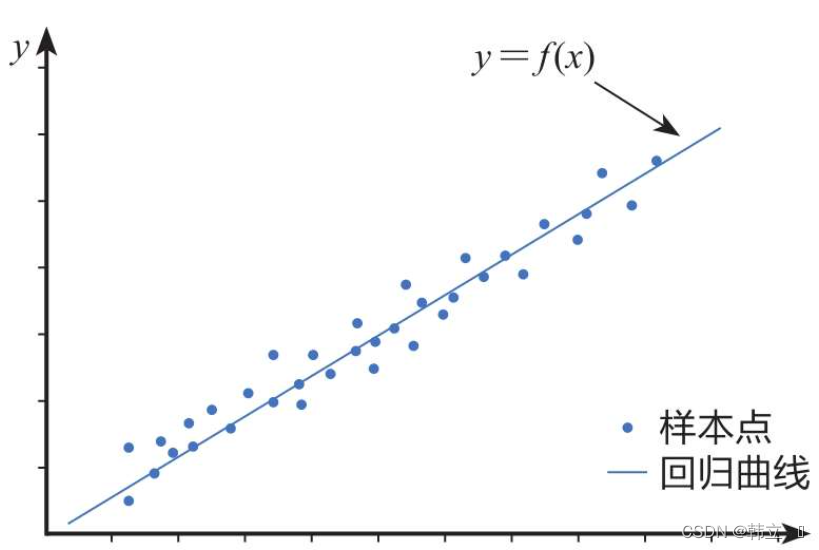
矩阵运算 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import numpy as npa=np.array([[1 ,2 ,3 ],[4 ,5 ,6 ]]) b=np.array([[1 ,2 ],[3 ,4 ],[5 ,6 ]]) c=np.array([[1 ,2 ,3 ]]) d=np.array([[9 ,8 ,7 ],[3 ,2 ,1 ]]) sum =a+de=3 *a e=np.dot(a,b) e=a*d print (e)e=c.T print (e)e=np.array([[1 ,2 ],[3 ,4 ]]) result=np.linalg.inv(e) result=np.linalg.det(e) e=np.linalg.matrix_rank(d) print (e)
求一次方程组的解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import numpy as npfrom sympy import symbols,Eq,solveA=np.array([[10 ,-1 ,-2 ],[-1 ,10 ,-2 ],[-1 ,-1 ,5 ]]) b=np.array([72 ,83 ,42 ]) inv_A = np.linalg.inv(A) x=inv_A.dot(b) x=np.linalg.solve(A,b) print (x)x,y,z=symbols('x y z' ) eqs=[Eq(10 *x-y-2 *z,72 ), Eq(-x+10 *y-2 *z,83 ), Eq(-x-y+5 *z,42 )] print (solve(eqs,[x,y,z]))
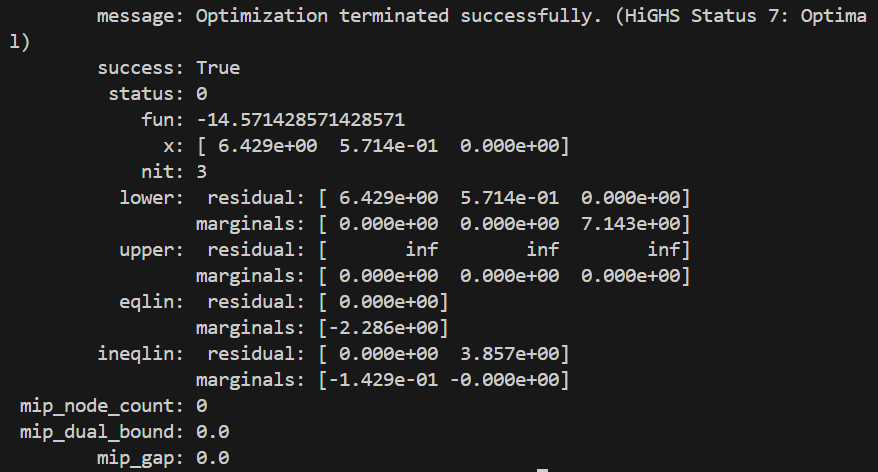
线性规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 from scipy import optimizeimport numpy as npc=np.array([2 ,3 ,-5 ]) A=np.array([[-2 ,5 ,-1 ],[1 ,3 ,1 ]]) b=np.array([-10 ,12 ]) Aeq=np.array([[1 ,1 ,1 ]]) beq=np.array([7 ]) x1=(0 ,None ) x2=(0 ,None ) x3=(0 ,None ) res=optimize.linprog(-c,A,b,Aeq,beq,bounds=(x1,x2,x3)) print (res)
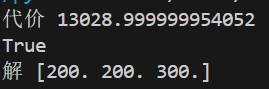
非线性规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 from scipy.optimize import minimizeimport numpy as npdef fun (x ): return (4 +0.3 *x[0 ]+0.0007 *x[0 ]*x[0 ]+3 +0.32 *x[1 ]*x[1 ]+3.5 +0.3 *x[2 ]+0.00045 *x[2 ]*x[2 ]) def con (): cons=({'type' :'eq' ,'fun' :lambda x: x[0 ]+x[1 ]+x[2 ]-700 }) return cons b1=(100 ,200 ) b2=(100 ,250 ) b3=(150 ,300 ) bnds=(b1,b2,b3) if __name__=="__main__" : cons=con() x0=np.array((150 ,250 ,20 )) res=minimize(fun,x0,method='SLSQP' ,constraints=cons,bounds=bnds) print ('代价' , res.fun) print (res.success) print ('解' ,res.x)
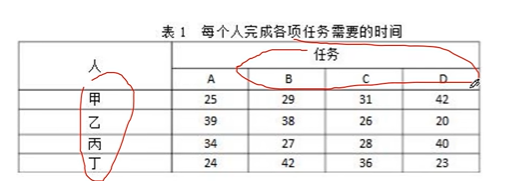
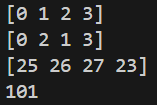
整数规划与指派问题
1 2 3 4 5 6 7 8 from scipy.optimize import linear_sum_assignmentimport numpy as npcost = np.array([[25 ,29 ,31 ,42 ],[38 ,39 ,26 ,20 ],[34 ,27 ,28 ,40 ],[24 ,42 ,36 ,23 ]]) row_id,col_id=linear_sum_assignment(cost) print (row_id)print (col_id)print (cost[row_id,col_id])print (cost[row_id,col_id].sum ())
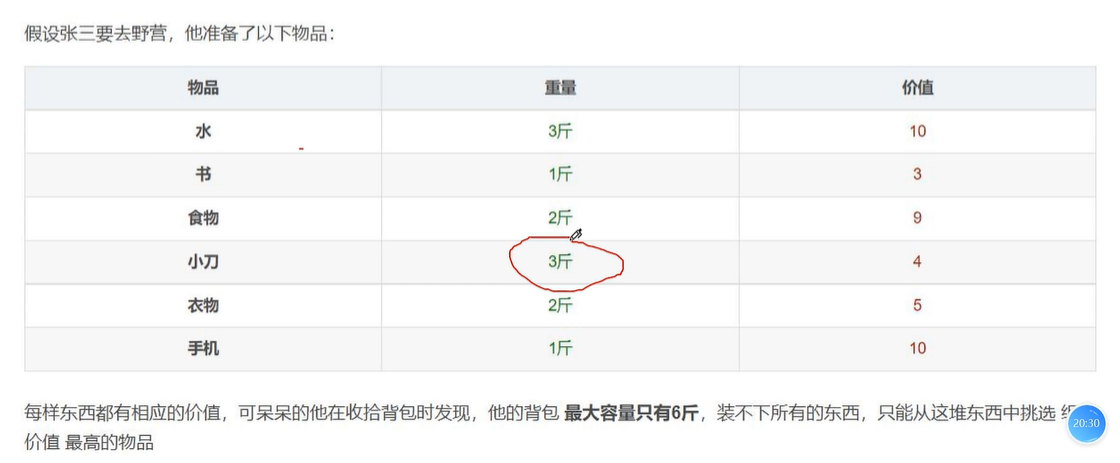
动态规划模型
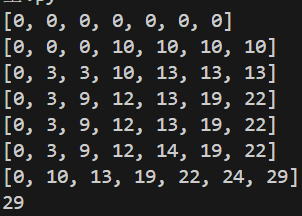
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 def dynamic_p ()->list : items=[ {"name" :"水" ,"weight" :3 ,"value" :10 }, {"name" :"书" ,"weight" :1 ,"value" :3 }, {"name" :"食物" ,"weight" :2 ,"value" :9 }, {"name" :"小刀" ,"weight" :3 ,"value" :4 }, {"name" :"衣物" ,"weight" :2 ,"value" :5 }, {"name" :"手机" ,"weight" :1 ,"value" :10 }, ] max_capacity=6 dp=[[0 ]*(max_capacity+1 ) for _ in range (len (items)+1 )] for row in range (1 ,len (items)+1 ): for col in range (1 ,max_capacity+1 ): weight=items[row-1 ]["weight" ] value=items[row-1 ]["value" ] if weight > col: dp[row][col]=dp[row-1 ][col] else : dp[row][col]=max (value+dp[row-1 ][col-weight],dp[row-1 ][col]) return dp dp=dynamic_p() for i in dp: print (i) print (dp[-1 ][-1 ])
在 Python 里,索引 -1 表示取列表的最后一个元素。所以 dp[-1][-1] 指的是二维列表 dp 中最后一行的最后一个元素。在动态规划场景下,像 0 - 1 背包问题,dp 数组往往会在完成所有状态转移之后,将最终的最优解存储在 dp[-1][-1] 这个位置。因此,print(dp[-1][-1]) 这行代码的作用就是把最终的计算结果打印出来。