第5章 分治法
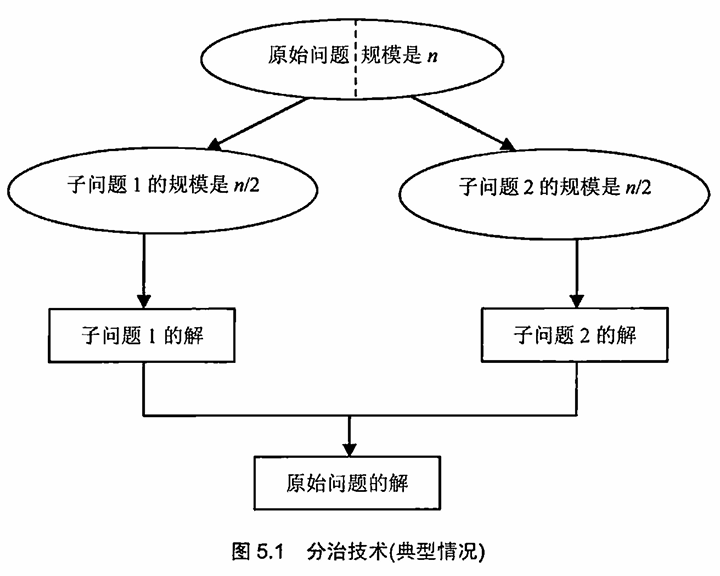
5.1 合并排序
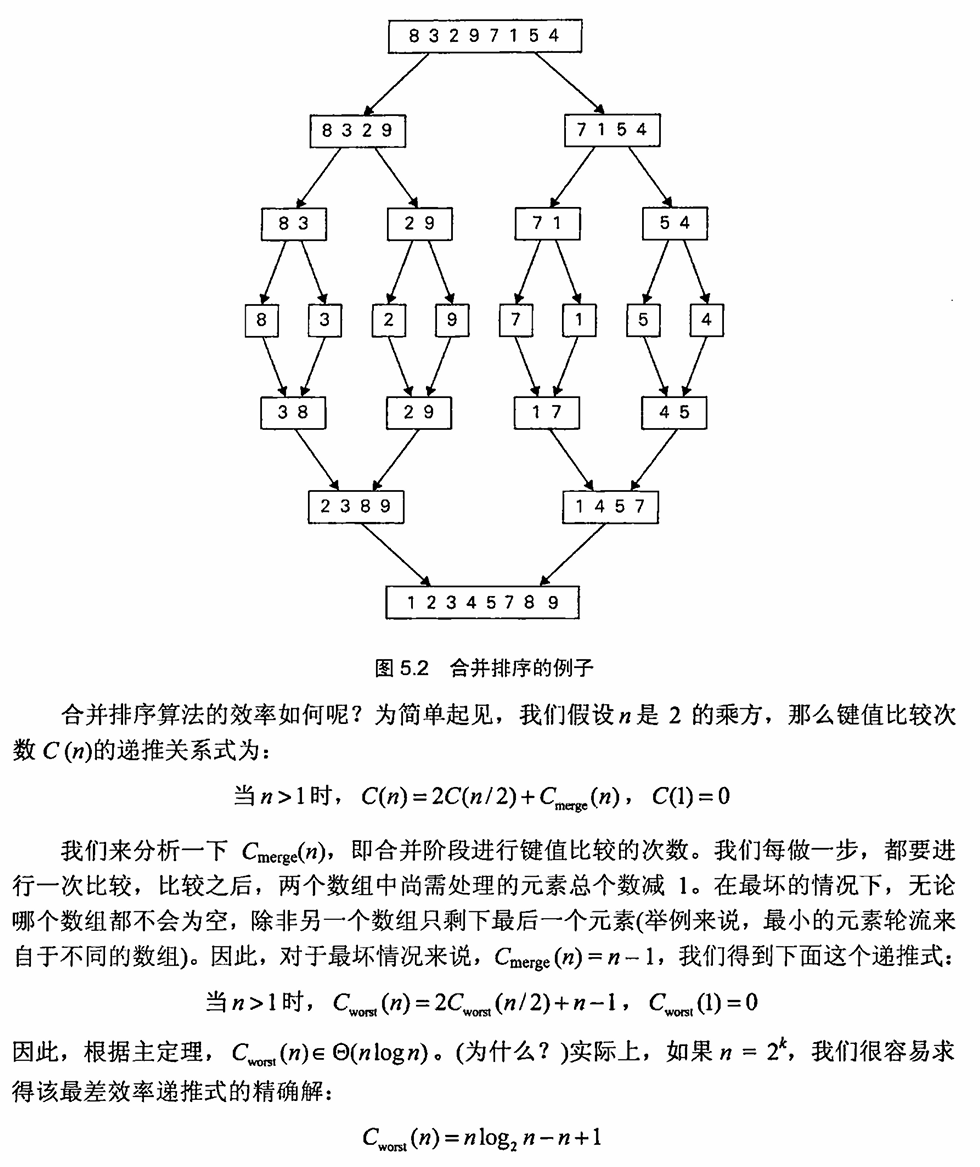
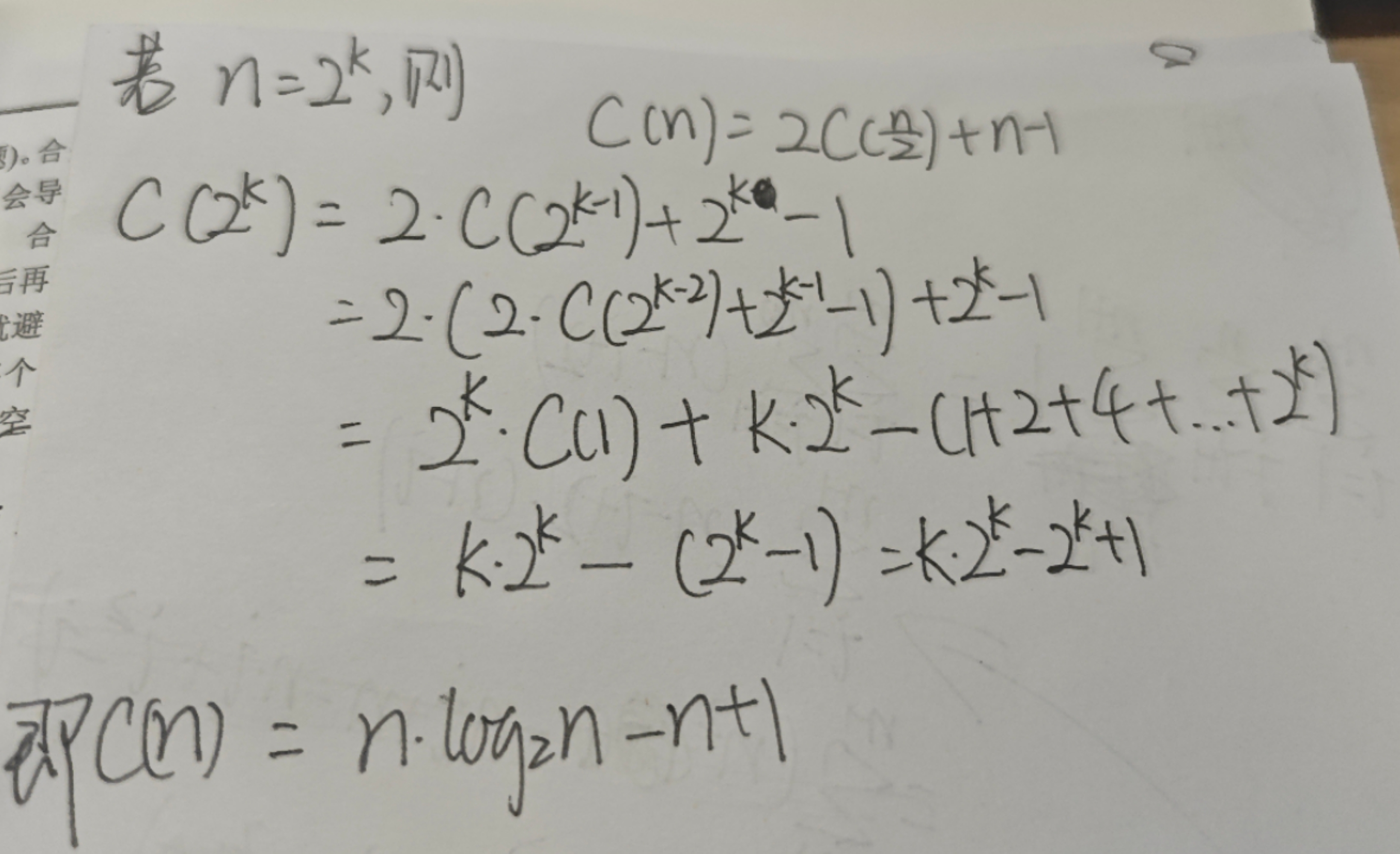
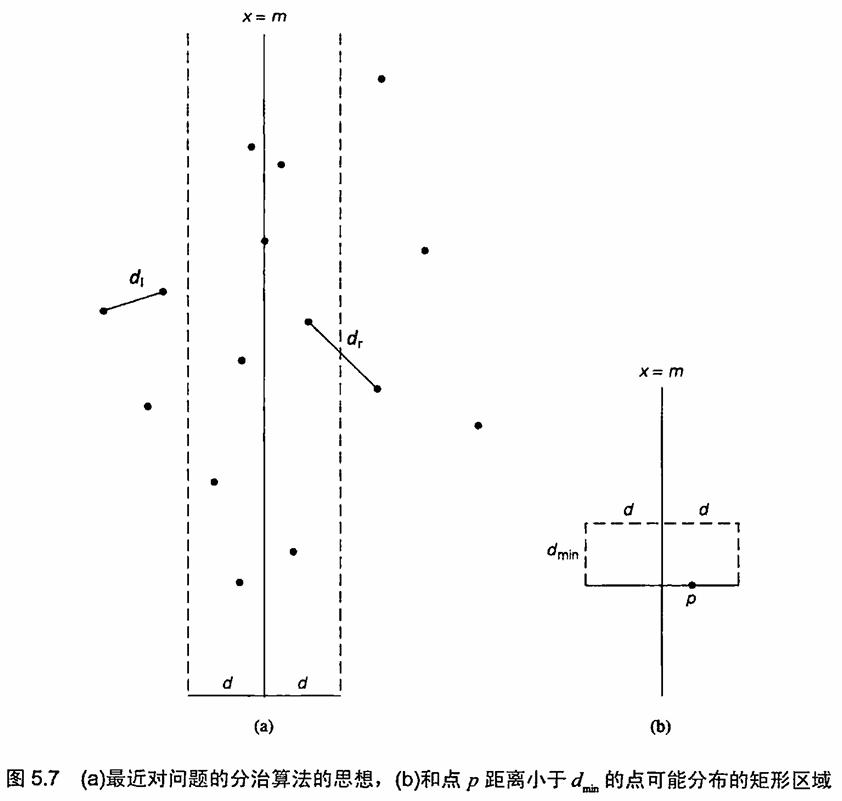
5.5 用分治法解最近对问题和凸包问题
最近对问题
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 Lee的学习之旅！
相关推荐
2025-02-09
C和C++的区别
2025-02-07
C++笔记
C++参考文档 课程链接：国外公认讲的最好的【C++教程】技术大佬带你从零基础入门到精通，油管百万级收藏，学C++看这个就够了！ 变量 变量类型 占用内存的字节数(byte) int 4 char 1 short 2 long 4 long long 8 float 4 double 8 bool 1 变量前加unsigned即舍弃符号位，能表示的数值的最大值为原来的两倍 字符 ASCII表上对应的值 0 48 a 97 A 65 例子： 1234567char a=65;cout<<a<<endl;//输出为字符A//------------------float b=5.5;//此时b为double类型float...
2025-02-27
第2章 算法效率分析基础
2.2 渐进符号和基本效率类型 类型按照增长次数的升序排列 2.4 递归算法的数学分析反向替代法 分析递归算法时间效率的通用方案 汉诺塔游戏 手写的详细步骤四个盘子时： 代码实现123456789101112131415161718192021222324252627282930#include <stdio.h>int m=0;void Move(int n,char A,char B,char C)//A和B柱并不固定，可以互换，A是盘子所在的塔，B是辅助塔，C是目标塔,函数的目的是把A上的n个盘子通过B全部转移到C{ m++; //设置移动盘子的结束条件（当只有一个盘子时直接从A或B柱移到C柱）,如果A当前还有一个盘子那么就把他直接移动到C if(n == 1) { printf("%c -> %c\n",A,C); } //否则开始递归 else ...
2025-02-27
第3章 蛮力法
3.2 顺序查找和蛮力字符串匹配顺序查找： 1234567891011121314151617181920#include<iostream>#include<cstring>using namespace std;int SequentialSearch(string& a,char b){ int i=0; while(i<a.length()&&a[i++]!=b); if(a[i-1]==b)i--; if(i<a.length())return i; else return -1;}int main(){ string a="abbbbc"; cout<<SequentialSearch(a,'d')<<endl; cin.get(); return...
2025-03-15
第4章 减治法
4.1 插入排序插排的代码可看数据结构中排序那部分 4.3 生成组合对象的算法Johnson-Trotter算法 1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677#include <iostream>#include <vector>// 检查元素是否可移动bool canMove(const std::vector<int>& perm, const std::vector<int>& dir, int index) { int d = dir[index]; if (d == -1 && index > 0 && perm[index] > perm[index - 1]) { ...
2025-01-01
第1章 绪论
欧几里得算法求m和n的最大公约数 12345678910111213//欧几里得算法（求最大公约数）int Euclid(int m, int n){ if (m <= 0 || n <= 0)return -1; int r = 0; while (n != 0) { r = m % n; m = n; n = r; } return m;} 埃拉托色尼筛选法找出不大于n的质数序列 1234567891011121314151617181920212223242526272829303132//埃拉托色尼筛选法vector<int> Sieve(int n){ vector<int> A; A.push_back(0);A.push_back(0); vector<int> L; int j = 0; for (int p = 2;p <= n;p++) { A.push_back(p); } for (int p = 2;p * p...
