一元线性回归分析模型
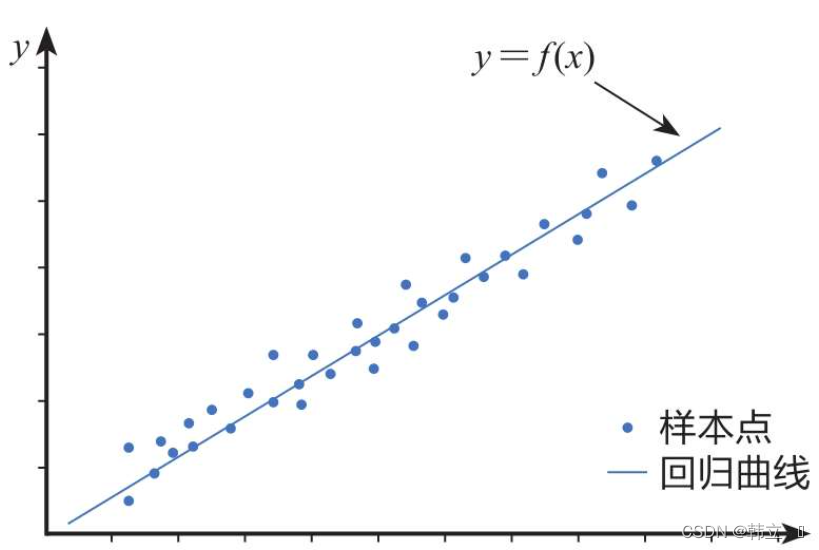
原理一元线性回归分析模型(Simple Linear Regression Model)是一种统计方法,用于研究两个连续变量之间的关系:一个因变量(通常记为 (Y))和一个自变量(通常记为 (X))。这个模型假设这两个变量之间存在线性关系,并试图通过最小化预测值与实际观测值之间的差异来拟合一条直线。 残差图作图命令:rcoplot(r,rint) 建模步骤 数据收集:首先需要收集包含因变量和自变量的数据集。 模型设定:设定一元线性回归模型的形式,即 (Y = \beta_0 + \beta_1 X + \epsilon)。 参数估计:使用最小二乘法(Ordinary Least Squares, OLS)等方法来估计未知参数 (\beta_0) 和 (\beta_1)。OLS的目标是找到使残差平方和最小化的参数值,即 (\sum (Y_i - (\beta_0 + \beta_1 X_i))^2)...
图论模型
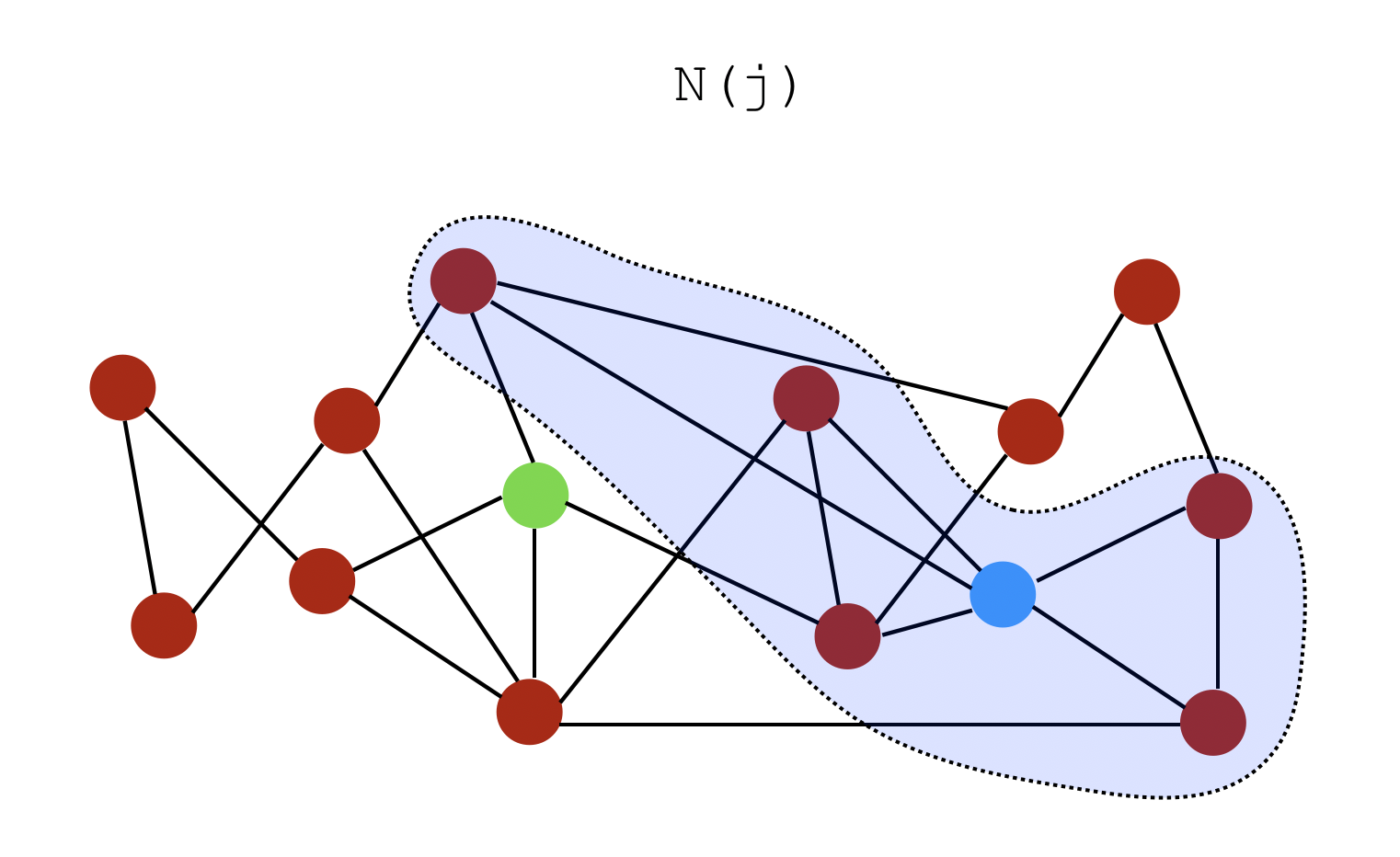
Matlab作无向图(1)无权重(每条边的权重默认为1)函数**graph(s,t)**:可在 s 和 t 中的对应节点之间创建边,并生成一个图 s 和 t 都必须具有相同的元素数;这些节点必须都是从1开始的正整数,或都是字符串元胞数组。 注意哦,编号最好是从1开始连续编号,不要自己随便定义编号 123456789101112131415s1 = [1,2,3,4];t1 = [2,3,1,1];G1 = graph(s1, t1);plot(G1)% 下面的命令是在画图后不显示坐标set( gca, 'XTick', [], 'YTick', [] ); % 注意字符串元胞数组是用大括号包起来的哦s2 = {'学校','电影院','网吧','酒店'};t2 = {'电影院','酒店','酒店','KTV'};G2 = graph(s2,...
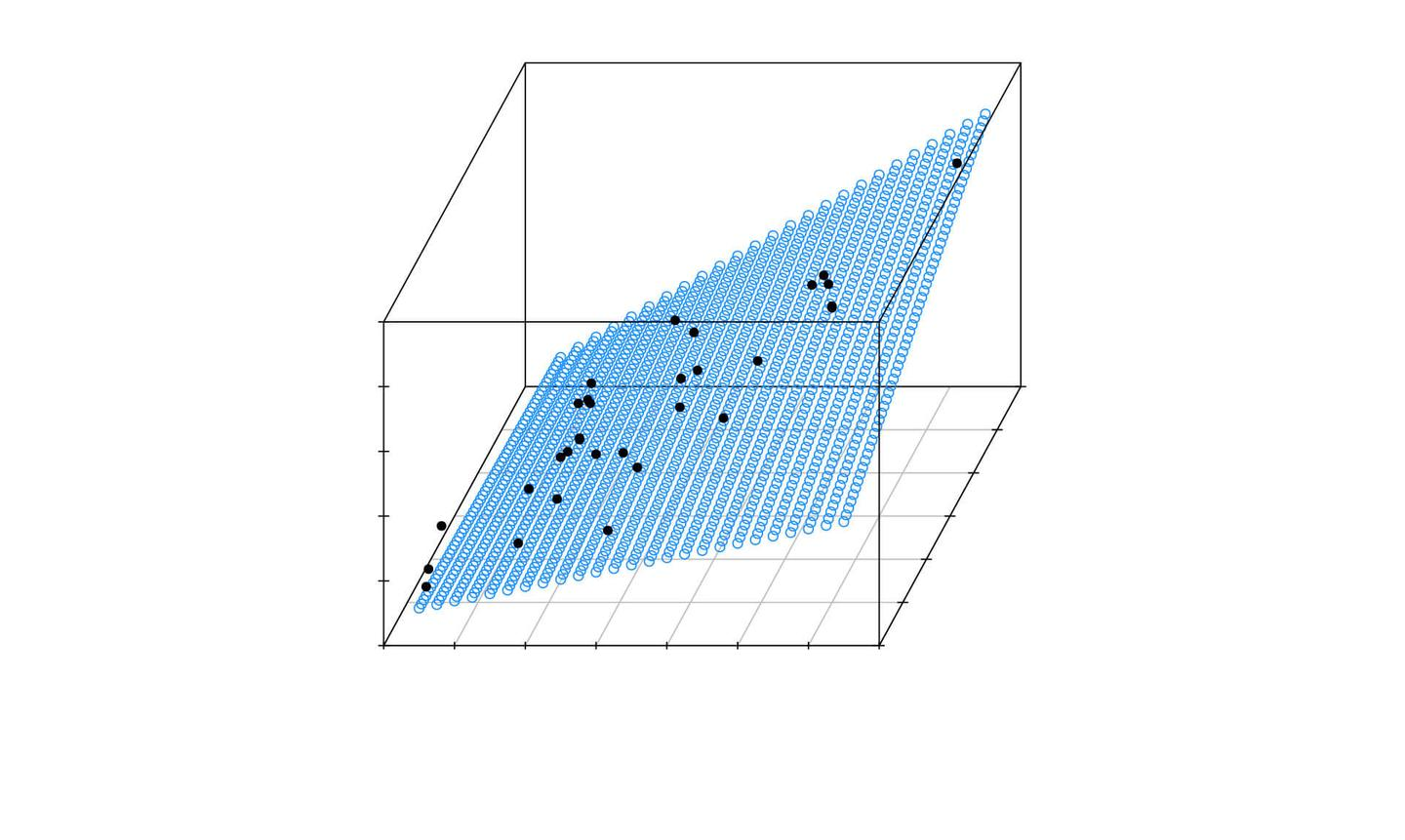
多元线性回归分析模型
...
动态规划模型
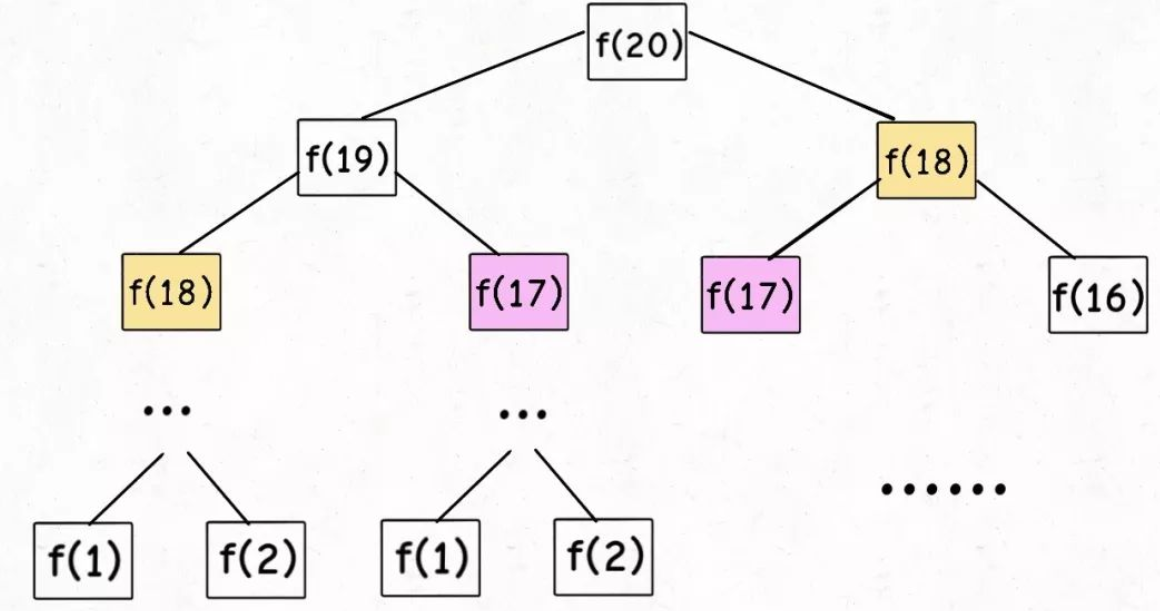
原理动态规划(Dynamic...
多目标规划模型
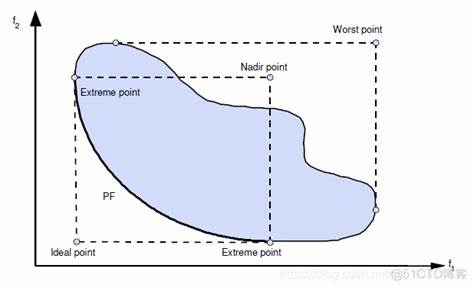
原理多目标规划模型是一种数学建模方法,它允许决策者同时优化多个目标函数。在现实世界的问题中,通常会遇到需要同时考虑多个不同且常常相互冲突的目标的情况。例如,在一个企业资源分配问题中,可能希望最大化利润的同时最小化成本和环境影响。 解决多目标规划问题的方法有很多,包括但不限于: 加权和法:将所有目标通过赋予不同的权重组合成一个单一的目标函数进行优化。 ε-约束法:选择一个目标作为主要目标进行优化,而其他目标则被转化为约束条件。 帕累托最优解集:寻找不是由任何其他解决方案支配的解,即帕累托前沿上的点。 进化算法:如遗传算法、粒子群优化等,它们可以用来近似找到帕累托最优解。 妥协规划:通过定义理想点和计算每个可行解与理想点的距离来找到最佳折衷解。 每种方法都有其适用场景和局限性,选择哪种方法取决于具体问题的特点以及决策者的偏好。 代码 多目标规划问题123456789w1 = 0.4; w2 = 0.6; % 两个目标函数的权重 x1 = 5 x2 = 2w1 = 0.5; w2 = 0.5; % 两个目标函数的权重 x1 = 5 x2 = 2w1 =...
时间序列模型(ARIMA)
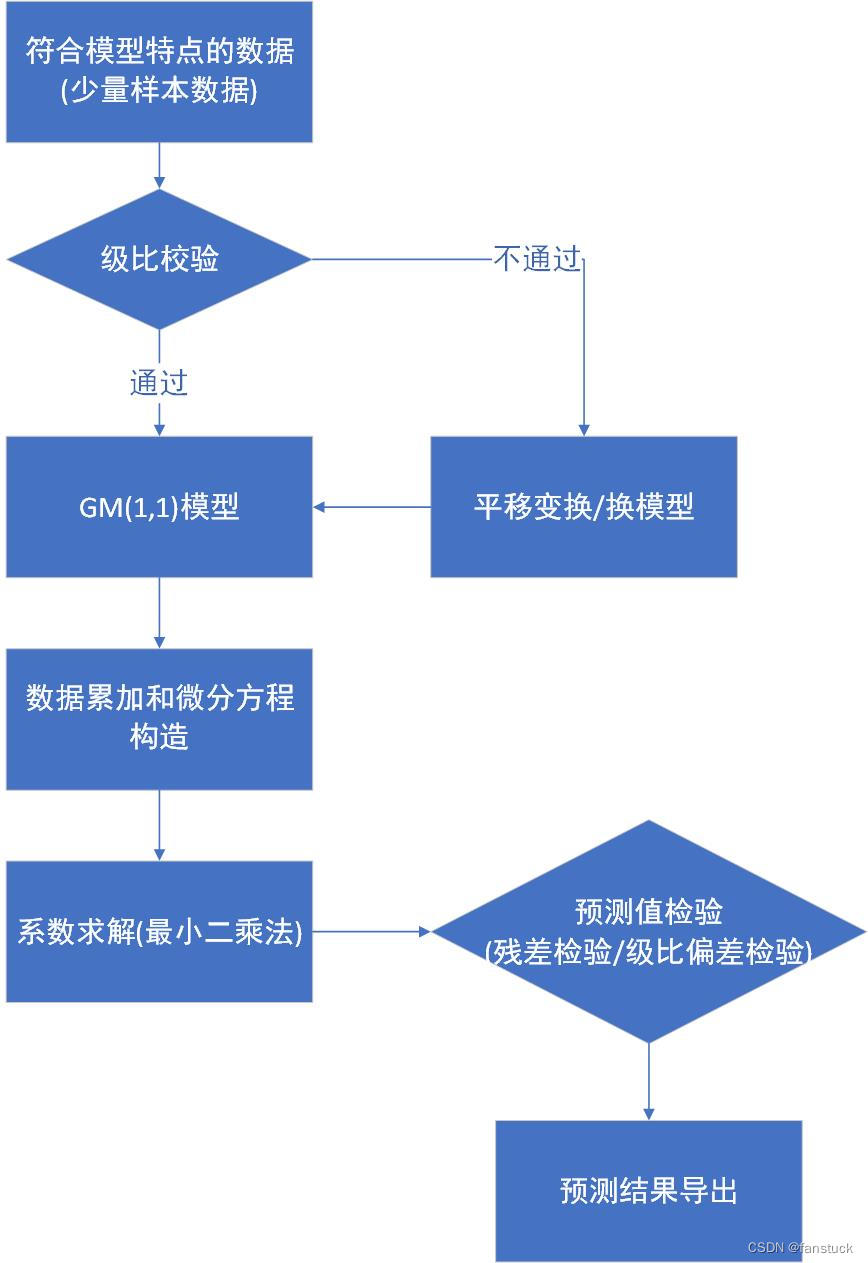
原理ARIMA模型,即自回归积分滑动平均模型(AutoRegressive Integrated Moving Average),是时间序列分析中用于预测的统计模型。它结合了三个主要组件:自回归(AR)、差分整合(I)和移动平均(MA)。ARIMA模型适用于非季节性数据,可以处理具有趋势和周期性的数据。 使用ARIMA模型:在实际应用中,ARIMA模型被广泛应用于金融、经济、气象等领域的时间序列预测。为了构建一个有效的ARIMA模型,通常需要经历以下步骤: 确定模型的阶数 p,d,qp,d,q。 对选定的模型进行参数估计。 检查模型的适应性,并根据需要调整模型。 利用最终确定的模型对未来值进行预测。 ARIMA模型也可以扩展到包含季节性因素的SARIMA(Seasonal ARIMA)模型,以及结合外生变量的ARIMAX模型。
非线性回归分析模型
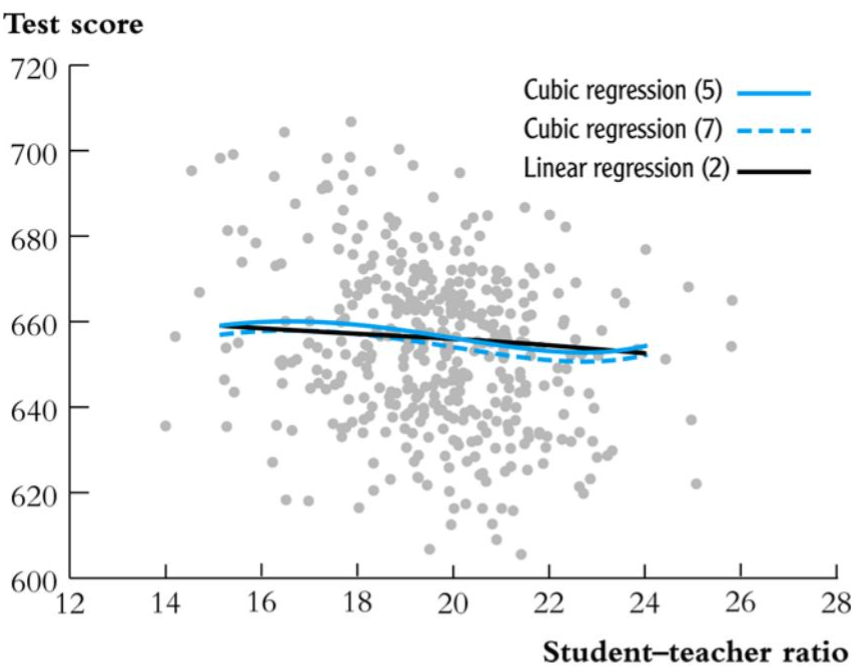
原理非线性回归分析是一种统计方法,用于研究因变量(响应变量)与一个或多个自变量之间的关系,当这种关系不是线性的而是曲线型时。在非线性回归中,因变量和自变量之间的关系通过一个非线性的函数来表达。这不同于多元线性回归,后者假设因变量是自变量的线性组合。 建立非线性回归模型的过程包括以下步骤: 选择模型:根据理论、经验或者数据探索选择适当的非线性函数形式。 参数估计:使用迭代算法(如高斯-牛顿法、Levenberg-Marquardt算法等)来寻找最佳拟合参数...
整数规划和0-1规划
原理整数规划(Integer Programming, IP)和0-1规划(Binary or Zero-One Programming)是运筹学中线性规划的两个特殊类型,它们在优化问题中用于寻找最优解。这类问题的特点是在决策变量上增加了整数或二进制(0或1)的约束条件。 整数规划整数规划是指在优化模型中,部分或全部决策变量被要求取整数值的问题。这与普通的线性规划不同,在线性规划中,决策变量可以取任何实数值。整数规划的一个重要子类是纯整数规划(Pure Integer Programming),其中所有决策变量都必须取整数值;而混合整数规划(Mixed Integer Programming,...
最小最大化模型
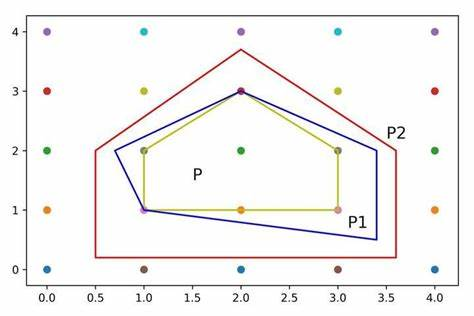
原理最小最大化模型(Minimax Model),是优化领域中的一种建模方法,主要用于决策制定过程中处理不确定性或对抗性环境。这类模型试图找到一种策略,使得最坏情况下的结果尽可能好。 Maximin 模型在maximin模型中,目标是选择一个策略,以确保即使是在最不利的情况下,也能获得尽可能好的结果。换句话说,就是从所有可能的最差结果中选取最好的一个。这种模型常用于保守决策者希望最小化其潜在损失的情境中。 应用例子: 投资组合选择:投资者可能会使用maximin模型来选择投资组合,以保证即使市场表现最糟糕时,他们也能获得一定的回报。 军事战略:指挥官可能采用maximin模型来规划战术,确保即便面对敌方的最佳反击,己方仍能维持最低限度的成功。 Minimax...