主成分分析法
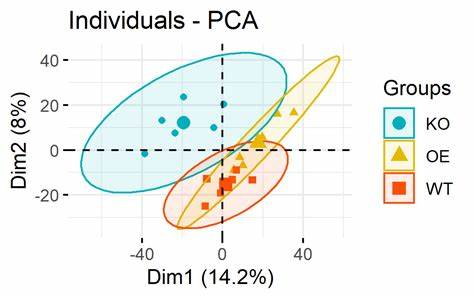
原理主成分分析法(Principal Component...
非线性规划模型
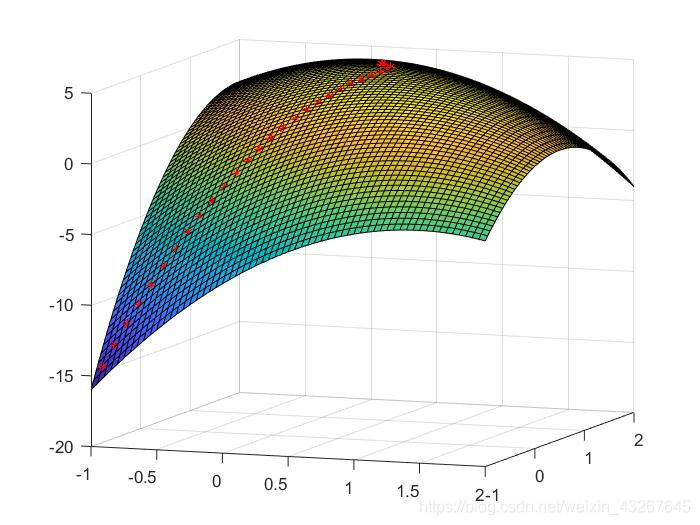
原理非线性规划(Nonlinear Programming, NLP)模型是一类优化问题,其中目标函数或约束条件至少有一个是非线性的。非线性规划问题的目标是在满足一组约束条件的前提下,最小化或最大化一个非线性函数。 非线性规划模型的一般形式一个标准的非线性规划模型可以表示为: 123456minimize f(x)subject to:g_i(x) ≤ 0, i = 1, ..., mh_j(x) = 0, j = 1, ..., px_L ≤ x ≤ x_U 这里: f(x) 是需要最小化的非线性目标函数。 g_i(x) 是不等式约束函数。 h_j(x) 是等式约束函数。 x_L 和 x_U 分别是变量 x 的下界和上界,即变量范围约束。 x...
线性规划模型
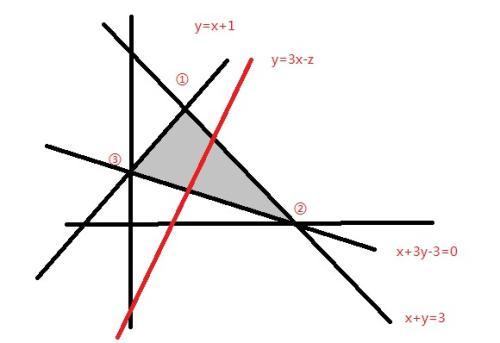
原理线性规划(Linear Programming, LP)是一种优化技术,用于在满足一系列线性不等式或等式的约束条件下,最大化或最小化一个线性目标函数。线性规划模型通常包含以下几个组成部分: 决策变量:这些是需要求解的未知数,它们代表了我们希望做出的决策。例如,在生产计划中,决策变量可能是每种产品的生产数量。 目标函数:这是我们需要优化的表达式,即最大化或最小化的函数。目标函数由决策变量的线性组合构成。例如,最大化利润或最小化成本。 约束条件:这些是限制决策变量值的线性不等式或等式。它们反映了资源的有限性、技术上的限制或其他实际操作中的要求。例如,原材料的数量、机器的工作时间等。 非负条件:通常情况下,决策变量不能取负值,因为这在许多实际问题中没有意义。比如,你不能制造负数量的产品。 线性规划问题可以表示为以下标准形式: 最大化或最小化目标函数 Z = c1x1 + c2x2 + ... + cnxn 满足约束条件 a11x1 + a12x2 + ... + a1nxn <= b1 `a21x1 + a22x2 + ... +...
蒙特卡洛法
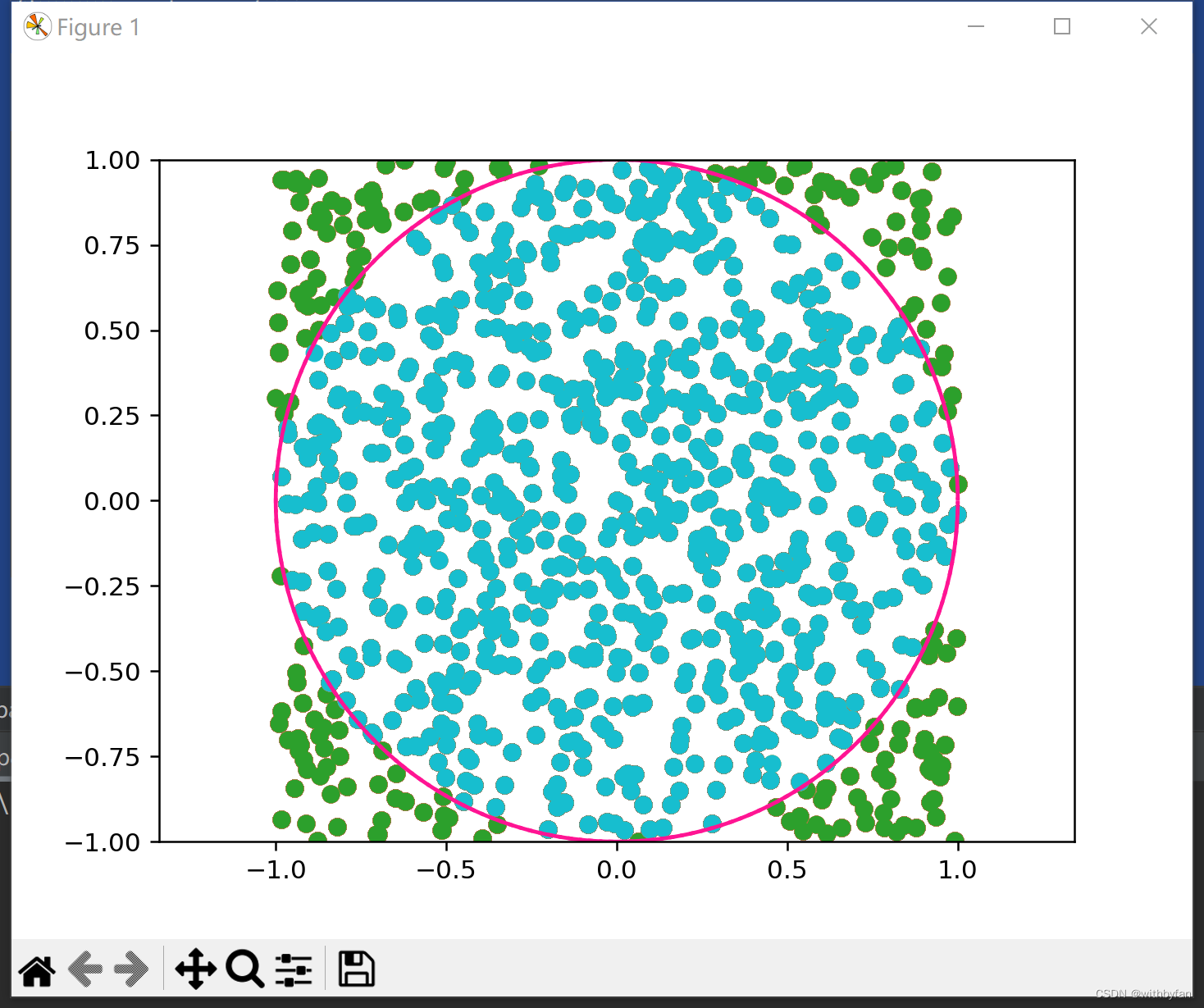
原理蒙特卡洛方法(Monte Carlo method)是一类用于解决各种问题的随机算法,广泛应用于数学、物理、工程、金融等领域。该方法以摩纳哥著名赌城蒙特卡洛命名,因为其核心思想依赖于随机抽样或统计抽样,类似于赌博中的随机性。 明确指令-拆解问题-分析生成什么是蒙特卡洛法?结论: 蒙特卡洛法是一种基于概率统计理论的数值计算方法,通过大量随机样本模拟来求解问题。 详细展开: 随机抽样: 蒙特卡洛方法利用随机数生成器产生大量的随机样本点,然后根据这些样本点来估计所研究的问题的解。 数值积分: 在无法解析地求出定积分时,可以通过蒙特卡洛方法来进行数值积分,即用随机点落在被积函数下的平均值乘以区域大小来近似积分值。 优化与仿真: 方法也常用于复杂系统的仿真和优化,如金融风险评估、粒子物理实验设计等。 误差估计: 随着样本数量的增加,蒙特卡洛方法给出的结果会逐渐收敛到真实值,且可以估算结果的不确定性或误差范围。 蒙特卡洛法的应用场景: 物理科学: 模拟粒子传输、热力学性质等。 金融工程: 计算期权定价、投资组合风险管理等。 计算机图形学:...
灰色关联分析
原理灰色关联分析(Grey Relational Analysis,...
北京大学编译实践课程
北京大学编译实践课程在线文档 开发环境
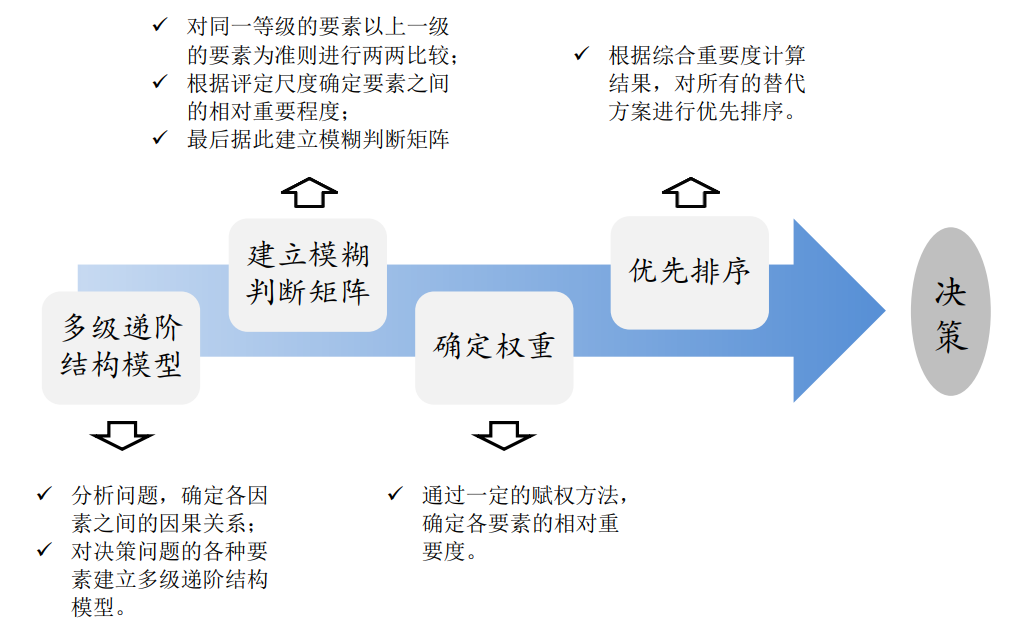
模糊综合评价
...
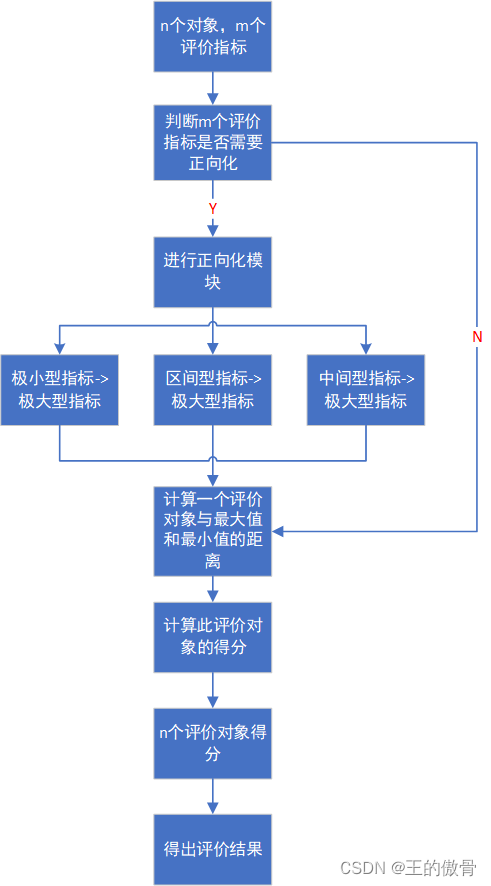
TOPSIS法
原理TOPSIS(Technique for Order Preference by Similarity to Ideal...
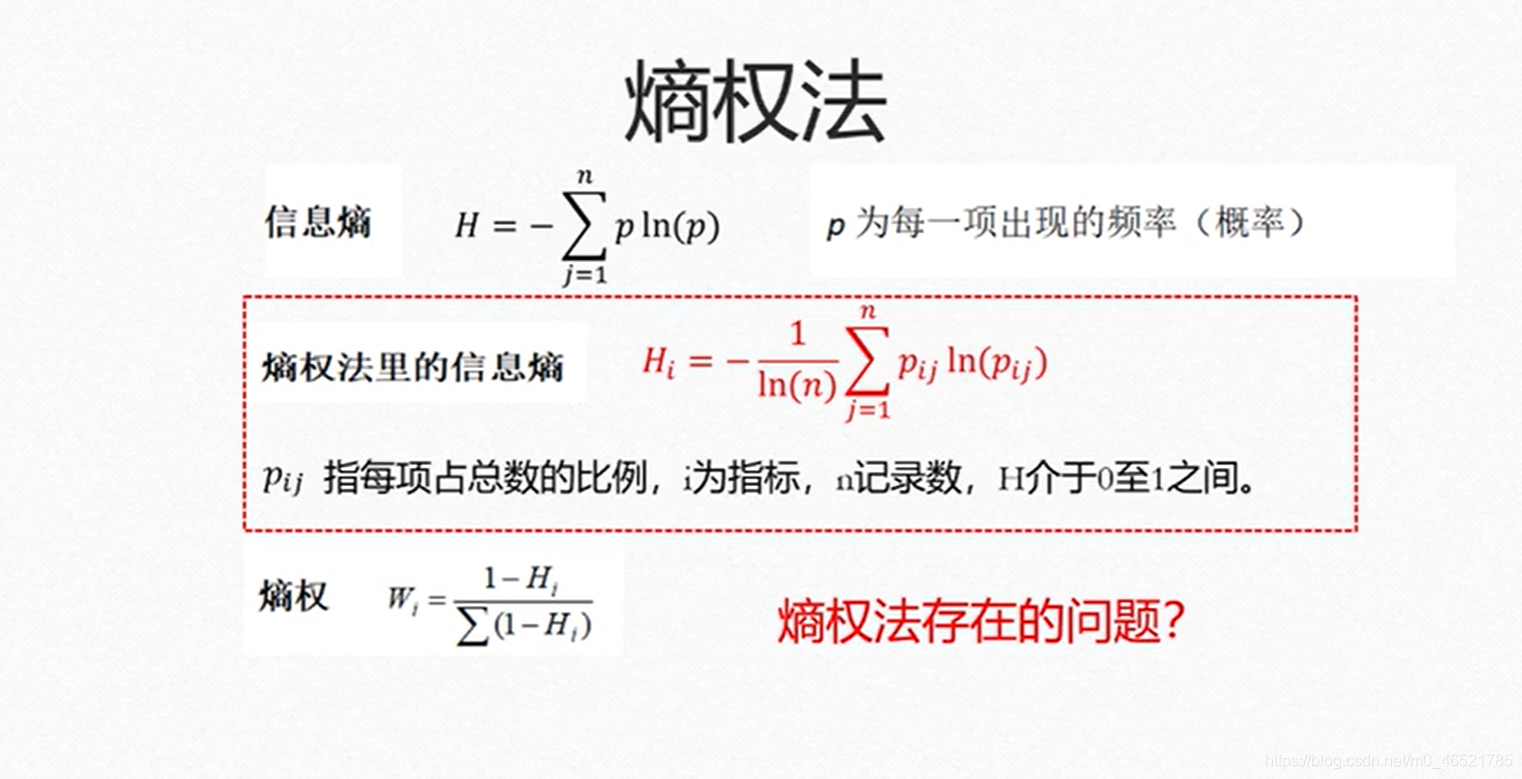
熵权法
...
第1章 绪论
欧几里得算法求m和n的最大公约数 12345678910111213//欧几里得算法(求最大公约数)int Euclid(int m, int n){ if (m <= 0 || n <= 0)return -1; int r = 0; while (n != 0) { r = m % n; m = n; n = r; } return m;} 埃拉托色尼筛选法找出不大于n的质数序列 1234567891011121314151617181920212223242526272829303132//埃拉托色尼筛选法vector<int> Sieve(int n){ vector<int> A; A.push_back(0);A.push_back(0); vector<int> L; int j = 0; for (int p = 2;p <= n;p++) { A.push_back(p); } for (int p = 2;p * p...