层次分析法
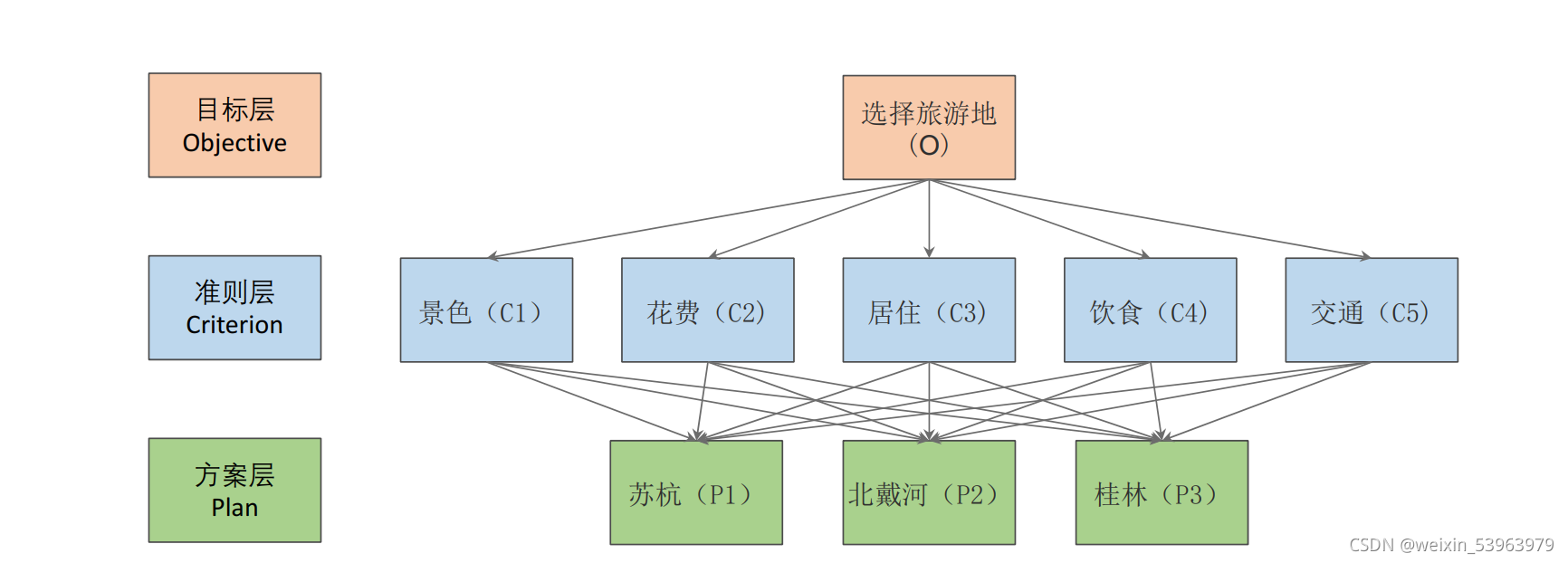
原理层次分析法(Analytic Hierarchy Process,简称AHP)是一种结构化的多准则决策制定方法。它是由美国运筹学家托马斯·萨蒂(Thomas L. Saaty)在20世纪70年代提出的。该方法通过将复杂的问题分解成多个层次的子问题,并对这些子问题进行两两比较,从而帮助决策者在多个备选方案中选择最优方案。 以下是使用层次分析法的基本步骤: 构建层次结构模型: 目标层:明确决策的目标。 准则层:确定达成目标所需的评价标准或准则。 方案层:列出所有可行的备选方案。 构造判断矩阵: 对于每一层中的元素,根据其相对于上一层某一元素的重要性,进行两两比较,构造出一个正互反矩阵(即判断矩阵)。比较时通常采用Saaty的1-9标度法来量化相对重要性。 计算权重向量和一致性检验: 计算每个判断矩阵的最大特征根及其对应的归一化特征向量,这个特征向量即为相应层各元素的权重向量。 进行一致性比率(Consistency Ratio,...
Git的基础操作指令
Git工作目录下对于文件的修改(增加、删除、更新)会存在几个状态,这些修改的状态会随着我们执行Git 的命令而发生变化。 添加文件至忽略列表一般我们总会有些文件无需纳入Git 的管理,也不希望它们总出现在未跟踪文件列表。 通常都是些自动 生成的文件,比如日志文件,或者编译过程中创建的临时文件等。 在这种情况下,我们可以在工作目录 中创建一个名为 .gitignore 的文件(文件名称固定),列出要忽略的文件模式。下面是一个示例: 123456789101112# no .a files *.a # but do track lib.a, even though you're ignoring .a files above !lib.a # only ignore the TODO file in the current directory, not subdir/TODO /TODO # ignore all files in the build/ directory build/ # ignore doc/notes.txt, but not...
一道关于足球的考察平面图知识的题目
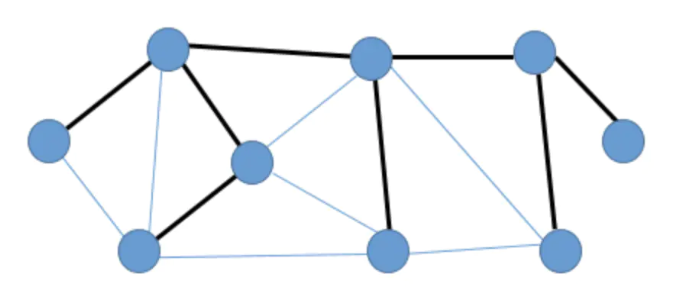
题目及解答 关于平面图概念离散数学中的平面图是一种特殊的无向图,它可以在平面上绘制而没有任何边交叉。换句话说,一个图如果可以嵌入到平面中,即可以在不使边交叉的情况下画在平面上,则该图称为平面图。 平面图的一些重要概念和定理包括: 库拉托夫斯基定理:这是判断一个图是否为平面图的一个标准。根据这个定理,一个有限图是平面图当且仅当它不包含K₅(完全五边形)或K₃,₃(完全二分图,两边各有三个顶点)作为子图的细分。也就是说,不能通过增加顶点将这些图变成原图的子图。 欧拉公式:对于任何连通的平面图,设V为顶点数,E为边数,F为面数(包括外部无限面),则有 V - E + F =...
最小生成树
算法步骤Prim Kruskal 代码123456789101112131415161718192021222324clc,clear% matlab中,不存在的边设置成0% 6个顶点,初始化定义6x6的全零矩阵作为邻接矩阵a = zeros(6);% 注意,最小生成树是针对无向图的,每条边权重只需要设一次。1到2和2到1是同一条边% 因此,可仅使用邻接矩阵的上三角矩阵来构造图Ga(1,[2 3])=[14 18]; % 顶点1到顶点2、3的边的权重a(2,[3:5])=[13 18 16]; % 顶点2到顶点3、4、5的边的权重a(3,[4 5])=[12 16]; % 同上。因为写过1到3,和2到3的边的权重,无需重复设a(4,[5 6])=[14 19]; a(5,6)=10;s=cellstr(strcat('城市',int2str([1:6]')));G=graph(a,s,'upper'); % 仅使用 A...
最短路径
算法步骤Floyd算法参考CSDN文章 Dijkstra Floyd 代码12345678910111213141516171819202122232425262728293031% 定义图的边和权重s = [9 9 1 1 3 3 3 2 2 5 5 7 7 8]; % 起始节点编号t = [1 2 2 3 4 6 7 4 5 4 7 6 8 6]; % 终止节点编号w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9]; % 边的权重% 创建一个图形对象 GG = graph(s,t,w);% 绘制图形 G,并将边的权重添加到图形上% G.Edges.Weight 表示图形对象 G 中所有边的权重值,'EdgeLabel' 表示在图形上显示这些权重值plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2)% 隐藏图形的坐标轴set( gca, 'XTick', [], 'YTick', [] );%...
证明无向图是连通图或者它的补图是连通图
补图的定义补图的数学定义为:对于一个给定的图G=(V,E),其补图G'=(V,E')是一个具有相同顶点集V的图,其中**E'是V中未出现在E中的所有可能边的集合**。换句话说,G'中的边是G中不存在的边。 例题: 证明过程要证明对于任何无向图G,要么G是连通的,要么它的补图G’是连通的,我们可以使用反证法。 定义: 一个无向图G=(V,E)是连通的,如果对于任意两个顶点u, v ∈ V,存在一条从u到v的路径。 无向图G的补图G’=(V,E’),其中E’包含所有不属于E的边,即如果(u,v) ∉ E,则(u,v) ∈ E’。 证明: 假设给定一个无向图G,它既不是连通图,其补图G’也不是连通图。这意味着在G中存在至少两个连通分量C1和C2,在G’中也存在至少两个连通分量C1’和C2’。 考虑G中的两个连通分量C1和C2,因为它们是不同的连通分量,所以不存在直接连接C1和C2中顶点的边,即对于所有的u ∈ C1和v ∈ C2,(u,v) ∉ E。根据补图的定义,这些不在E中的边都应该出现在E’中,即对于所有的u ∈ C1和v ∈...
离散数学中的其中几种证明题
(1) 结论: (2) (3)
排序算法的复杂度
各类排序算法的复杂度 任何需要交换相邻元素进行排序的排序算法平均都需要Ω(N^2)时间证明:
哈夫曼树和哈夫曼编码
哈夫曼编码是一种用于数据压缩的编码方式,它使用变长编码来表示数据源中的符号。频率较高的符号用较短的编码,频率较低的符号用较长的编码,从而达到减少总编码长度的目的。 编码过程 例子: 对字母进行哈夫曼编码时的性质: 1.每个字母对应元素叶节点的值是该字母出现的次数 2.出现次数越多的字符编码越短 3.不出现歧义的情况下编出来的码长度最短 4.编码结果不唯一,字母编出来的码可能不一样,但是长度肯定一样 参考b站视频:哈夫曼树和哈夫曼编码, 看完秒懂! 不会出现歧义原因:不存在任意一个元素节点出现在另一个元素节点的路径中 应用: 压缩文件 代码实现12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485#include <iostream>#include <queue>#include...
读公众号文章《小红书的一个用户救了我》有感,忆我与R星游戏
半佛仙人:小红书的一个用户救了我 文章的大致内容是在小红书有个叫做“小奈”的用户,因为她是被鉴定为智商二级,所以说话语言表达起来看着就像小孩子一样。她02年出生的,今年22岁,她在小红书发过很多篇笔记记录的都是自己攒钱想要买switch的经历。可能是被她坚持体现的童真所感动吧,大家在评论区里都很友善,都在积极地一起想要帮助小奈。看下来还是很令人感动的,评论区里大家都很友爱,小奈也很真诚,但是其实最令我有所感触的是当我看到小奈在幻想如果真的买到switch后会怎样,在那一刻我仿佛看到了小学和初中时的自己。 小学 在小学的时候我有一个iPad mini,我平时可以用它来看视频和玩游戏。小学时玩游戏外我还喜欢在爱奇艺上面看作者们上传的游戏视频,有一天我偶然地刷到了一个与gta5有关的游戏视频,我已经忘记了作者是谁了,反正当我看到游戏内容和游戏画面时马上就沦陷了,我被gta5的玩法和游戏画质所深深地吸引住了。于是我开始迷上了在爱奇艺里刷各种各样与gta5有关的游戏视频,我记得当时我最爱看一个叫“裴小峰”的游戏主播...